Elsa CHOI

Elsa CHOI

統計1-基本分佈和性質

4 minute read

Published:

一些基本描述統計

信賴區間

  • 已知/未知分佈；已知/未知變異數
  • 如果是90% 信賴區間，$\frac{z_\alpha}{2}=1.65$；
  • 如果是95% 信賴區間，$\frac{z_\alpha}{2}=1.96$；
  • 最後，如果是99% 信賴區間，$\frac{z_\alpha}{2}=2.58$。

$期望值E,方差var和協方差Cov$

$E$

  1. $E(X\pm Y)=E(X)\pm E(Y)$
  2. $E(aX)=aE(X)$
  3. $E(c)=c$
  4. $E(\bar X)=E(X_i) \quad \forall i$

$var$

  1. $var(c)=0$
  2. $var(aX)=a^2 var(X)$
  3. $var(X\pm Y)=var(X)+var(Y)-2Con(X,Y)$
  4. $var(\bar X)=\frac{var(X)}{n}$
  5. $var(X)=E(X^2)-E(X)^2$

cov

  1. $Cov(X,Y)$ is bilinear
  2. $Con(aX,bY)=ab Con(X,Y)$
  3. $Cov(X,Y)=E((X-E(X))(Y-E(Y)))=E(XY)-E(X)E(Y)$
  4. $var(X\pmY)=var(X)+var(Y)-2Con(X,Y)$
  5. $\rho=\frac{\rho}{\sqrt{var(X)} \sqrt{var(Y)}}$
  6. $X,Y$獨立, 則$Cov(X,Y)=0$


條件概率

\[P(A|B)=\frac{P(AB)}{P(B)}\]

  • P.41

  • 如果$A_1.A_2,A_3$不相容

\[P(A_1\cup A_2 \cup A_3|B)=\frac{P(A_1)}{P(B)}+\frac{P(A_2)}{P(B)}+\frac{P(A_3)}{P(B)}\]
  • 乘法公式
\[P(A_1A_2A_3\dots A_n)=\frac{P(A_1A_2)}{P(A_1)}\frac{P(A_1A_2A_3)}{P(A_1A_2)} \dots \frac{P(A_1A_2\dots A_{n})}{P(A_1A_2\dots A_{n-1})} P(A_1)\]
  • 貝叶斯公式
\[P(B_i|A)=\frac{P(B_i)P(A|B_i)}{ \sum_{j=1}^n P(B_j)P(A|B_j)}\]

一些基本的分佈

離散

二次項分佈

  • wiki
  • $n$次伯努利分佈
\[f(k,n,p)= \text{Pr}(X=k)=\tbinom {n}{k}(1-p)^{n-k}p^{k}\]
  • 平均值和變異數
\[\text{E}(X)=np,\quad \text{var}(X)=np(1-p)\]

幾何分佈

  • wiki
  • 如果每次試驗的成功概率是$p$，那麼$k$次試驗中，第$k$次才得到第一次成功的概率是，
\[\text{Pr}(X=k)= (1-p)^{k-1}p\]
  • 平均值和變異數
\[\text{E}(X)=\frac{1}{p},\quad \text{var}(X)=\frac{1-p}{p^2}\]

超幾何分佈

wiki 超幾何分佈是統計學上一種離散概率分佈。它描述了由有限個物件中抽出$n$個物件，成功抽出指定種類的物件的個數（不歸還 （without replacement））。

例如在有$N$個樣本，其中$K$個是不及格的。超幾何分佈描述了在該$N$個樣本中抽出$n$個，其中$k$個是不及格的機率：

\[f(k;n,K,N)=\frac{\tbinom {K}{k} \tbinom {N-K}{n-k} }{\tbinom {N}{n} }\]

上式可如此理解：$\tbinom {N}{n}$ 表示所有在 $N$個樣本中抽出$n$個的方法數目。$\tbinom {K}{k}$表示在$K$個樣本中，抽出$k$個的方法數目，即組合數，又稱二項式係數。剩下來的樣本都是及格的，而及格的樣本有$N-K$個，剩下的抽法便有$\tbinom {N-K}{n-k}$種。

若$n=1$，超幾何分佈還原為伯努利分佈。其中 $k = 1, 2, 3, ….$

  • 平均值和變異數
\[\text{E}(X)=n\frac{K}{N},\quad \text{var}(X)=n\frac{K(N-K)(N-n)}{N^2(N-1)}\]

poisson分佈

\[\text{Pr}(X=k)=\frac{e^{-\lambda}\lambda^k}{k!}\]

卜瓦松分佈的母數$\lambda$是單位時間（或單位面積）內隨機事件的平均發生率。

  • 平均值和變異數
\[\text{E}(X)=\lambda,\quad \text{var}(X)=\lambda\]
  • 在一個固定時間間隔，或固定範圍內，觀察某一特定事件發生的次數，會發生幾次是一個隨機變數。

  • 在二項隨機試驗中，當$n$很大而$p$很小時，我們可以用卜瓦松分配求得二項分配的近似機率值(Simeon D. Poisson(1837), 1781~1840)，此時取

    \[\lambda=np\]
  • 我們想像這樣一個白努利隨機試驗，每此投擲銅板的時間間隔是相同的$h$，所以，當$n$很大時，這個投擲實驗像是在一個綿密的持續時間為$nh$的區間內，做觀察某一個特定事件(成功)出現的次數。二項隨機實驗是這$n$伯努利試驗的和，具有
    1. 每一次試驗彼此相互獨立，
    2. 成功的次數與持續時間$nh$ 成正比，
  • 這兩點性質滿足前面提到卜瓦松分配三個性質的(a)與(c)。當$p$很小時，這意謂接連兩次正面的機率非常非常地小，也就滿足(b)的性質。以上說明，當$n$很大而$p$很小時，二項隨機實驗的觀察機制非常類似卜瓦松隨機實驗，這也就是為什麼 Poisson(1837)得出可以用卜瓦松分配求得二項分配的近似機率值。

連續分佈

常數分佈

\[E(X)=\frac{b+a}{2} \quad var(X)=\frac{b-a}{12}\]

指數分佈

\[f(x)=\lambda \exp(-\lambda x) \quad x > 0\] \[E(X)=\frac{1}{\lambda},\quad var(X)=\frac{1}{\lambda^2}\]

正態分佈

\[f(x)=\frac{1}{\sqrt{2\pi \sigma} }\exp{-\frac{(x-\mu)^2}{2\sigma^2}}\]


統計特徵量

  • 用來表達所有資料中意涵訊息的特徵，以凸顯資料所代表的意義，讓使用該資料之研究者或讀者能夠掌握分析方向
  • 分四大類：集中量數、差異量數、偏態與峯度。

集中量數/集中趨勢量數

  • 指一羣體中之個體的某一特性，有其共同的趨勢存在，此一共同趨勢之量數即稱之集中趨勢量數
  • 因其能夠代表該羣體特性的平均水準，故通稱為平均數
  • 居有簡化作用、代表作用和比較作用

偏度

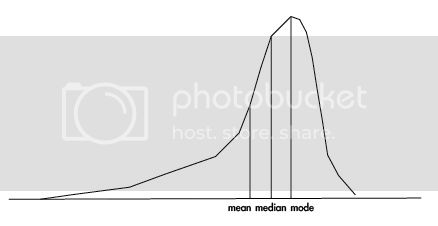
  • 負偏態或左偏態：偏度<0，平均值左側的橫軸更長，分佈的主體集中在右側。平均<中位<眾數，峯的位置在右邊。
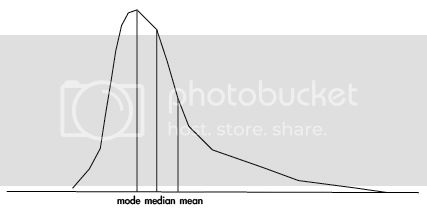
  • 正偏態或右偏態：偏度>0，平均值右側的橫軸更長，分佈的主體集中在左側。眾數<中位<平均，峯的位置在左邊。
\[g=\frac{m_3}{m_2^\frac{3}{2}}=\frac{\sum\limits_{i=1}^n (x-\bar x)^3}{(\sum\limits_{i=1}^n (x-\bar x)^2)^{\frac{2}{3} } }\]

峯度

  • wiki
  • 如果超值峯度為正，稱為尖峯態（leptokurtic）。如果超值峯度為負，稱為低峯態（platykurtic）。
\[g=\frac{m_4}{m_2^2}-3=\frac{\sum\limits_{i=1}^n (x-\bar x)^4} {(\sum\limits_{i=1}^n (x-\bar x)^2 )^2}-3\]
  • “減3”是為了讓正態分佈的峯度為0

相對分散度

  • 若有兩組資料而欲比較其相對分散程度時,會使用相對分散度來對比
\[\text{CV}=\frac{\sigma}{\mu}\]

異衆比率

\[V_r=\frac{ (\sum f_i ) -f_m}{\sum f_i}\]
  • 分子是非眾數的頻數和
  • 分母是全部眾數的頻數和

樣本分位數與樣本中位數

  • 數列下標由1開始
\[m_{0.5}=\Big\{ \begin{aligned} & x_{\frac{n+1}{2}} \quad & \text{n is odd}\\ & 0.5*(x_{\frac{n}{2}} +x_{\frac{n}{2}+1}) \quad & \text{n is even} \end{aligned}\] \[m_{p}=\Big\{ \begin{aligned} & x_{ \lfloor np+1 \rfloor]} \quad & np\text{ is not an integer}\\ & 0.5*(x_{np} +x_{np+1}) \quad & np \text{ is an integer} \end{aligned}\]

五數概括與箱線圖

\[x_{\text{min}}, Q_1=m_{0.25},m_{0.5},Q_3=m_{0.75},x_{\text{max}}\]
  • 當數據含有極端值時, 使用中位數比使用均更好,中位數的這種抗干擾性在統計中稱為具有穩健性

一些基本定理

中央極限定理

  • 中心極限定理就是研究隨機變量和的極限分布在甚麽條件下為正態分布的問題
\[\frac{\sum X_i-E(\sum X_i)}{ \text{Var}(\sum X_i)}= \frac{\sum X_i -n\mu}{\sigma\sqrt{n}}= \frac{\frac{\sum X_i}{n} -\mu}{\frac{\sigma}{\sqrt{n}}} \rightarrow N(0,1)\]

柴比雪夫不等式

\[\text{Pr}(|X-E(X)|\geq b) \leq \frac{\text{Var}(X)}{b^2}\]

或者

\[\text{Pr}(| \frac{\bar X-\mu}{\frac{\sigma}{\sqrt{n}}}|\geq b ) \leq \frac{1}{b^2}\]

大數法則

  • 大數定律討律的是在甚麽條件下, 隨機變量序列的算術平均依概率收斂到其均值的算術平均

  • 大數法則

\[\lim_{n\rightarrow \infty} P(\vert \frac{1}{n} \sum _{i=1}^n X_i -\frac{1}{n} \sum _{i=1}^n E(X_i) \vert \geq \epsilon) =0\]
  • 弱大數是極限的趨向是弱
  • 強大數是極限的趨向是強


三大分佈

$\chi^2$分布

  • P.283
  • 卡方：名義測量類型的數據
  • 卡方：單個總體的方差檢驗
  • 卡方圖形在$y$軸右側
  • 總體方差服從卡方分佈
  • $X_i \sim N(0,1)$
\[\chi^2=X_1^2+X_2^2+\dots +X_n^2\]
  • $x_i$是來自$N(\mu,\sigma)$樣本
  • $\bar x=\frac{1}{n}\sum x_i$
  • $s^2=\frac{1}{n-1}\sum(x-\bar x)^2$
\[\frac{(n-1)s^2}{\sigma^2} \sim \chi^2(n-1)\]

$F$分布

\[X_i\sim \chi^2(m),X_2 \sim \chi^2(n)\] \[F=\frac{X_1/m}{X_2/n}\] \[F_\alpha(n,m)=\frac{1}{F_{1-\alpha}(m,n)}\]
  • 若$x_1,\dots x_n \sim N(\mu_1, \sigma)$,$y_1,\dots y_n \sim N(\mu_2, \sigma)$
\[F=\frac{\frac{(m-1)s_x^2}{\sigma}}{\frac{(n-1)s_y^2}{\sigma}} =\frac{s_x^2}{s_y^2} \sim F(m-1,n-1)\]

$t$分布

  • 正態性、連續變量、獨立性和方差齊性

  • $X_1 \sim N(0,1),X_2\sim \chi^2(n)$,則

\[t=\frac{X_1}{\sqrt{X_2/n}}\]
  • $x1,\dots, x_n N(\mu,\sigma)$,$\bar x , s^2$是樣本的平均和方差,則
\[t=\frac{\sqrt{n}(\bar x -\mu)}{s}\sim t(n-1)\]

參數估計

  • $ \hat \theta$ 是估計出來
  • $\theta$ 是參數

矩法估計

  1. 樣本矩代替總體矩，矩可以是中心矩或原點矩
  2. 其估計參數和總體矩的函數, 亦用估計參數和樣本矩代替
\[E(X)=\frac{1}{\theta} \implies \bar X=\frac{1}{\hat \theta}\]

極大似然估計

  • $f$ 為概率函數
\[L(\theta)=L(\theta,X_1,X_2,\dots,X_n)=f(x_1,\theta)f(x_2,\theta)\dots f(x_n,\theta)\] \[L(\hat \theta)=\max_{\theta} L(\theta)\]

相合性

  • 相合性是滿足以下:
\[lim_{n \leftarrow \infty} P{ | \hat \theta -\theta| \geq \epsilon} =0\]
  • 定理, 若滿足以下
\[lim_{n \leftarrow \infty} E(\hat \theta) = \theta , \quad lim_{n \leftarrow \infty} Var(\hat \theta) = 0\]

則$\hat \theta$ 是相合

無偏性

\[E(\hat \theta)=\theta\]
  • 刀切法(Jackknife)
    • P304
    • 有空看一下

有效性

若$\text{Var}(\theta_1)<= \text{Var}{\theta_2}$,則稱$\theta_1$比$\theta_2$更有效

假設檢驗

  • $H_0$ VS $H_1$採用反證法的邏輯，假設$H_0$是對的，再看有沒有證據反對這個小概率的$H_0$
  • 應用了小概率原理
  • 不同的問題需要使用不同的檢驗統計量
  • 定義拒絕域$\bar W$，通常與$H_1$的$\leq,\geq$ 方向相同，暫時假設 $H_1 : x < 110 $，下面沿用這個$H_1$。

  • 顯著水平$\alpha$是一個概率值，

    \[\text{Pr} \{x \in \bar W \}=\alpha ，此時\bar W=\{ x<x_\alpha \}\]
  • $\alpha$亦表示原假設爲真時，拒絕原假設的概率。

  • p-value:落在與樣本計算出來的參數界限值$x_p$與$\bar W$的同方向的一邊的概率。用數學式表示則是

    \[p=\text{Pr}\{x<x_p \}\]

  • 所以當$p\leq\alpha$，即拒絕域

    \[\{x<x_p\} \subseteq\bar W\]
  • 置信水平$1-\alpha$提高，根據下式，置信距間變大
\[\text{Pr}(\text{置信距間})=1-\alpha\]
  • 樣本減少，$p$值增大

大樣本檢驗

  • p.384
\[\begin{aligned} I \quad &H_0:\theta \leq \theta_0 \quad &VS\quad &H_1:\theta > \theta_0 \\ II \quad &H_0:\theta \geq \theta_0 \quad &VS\quad &H_1:\theta < \theta_0 \\ III \quad &H_0:\theta = \theta_0 \quad &VS\quad &H_1:\theta \neq \theta_0 \end{aligned}\]
  • 二點分布$b(1,\theta)$ ,方差$\theta(1-\theta)$
\[u=\frac{\sqrt{n}(\bar x-\theta_0)}{\sqrt{\sigma^2(\hat \theta)}} \sim N(0,1)\]
  • possion
\[H_0:\lambda \leq \lambda_0 \quad VS \quad H_1:\lambda > \lambda_0\] \[u=\frac{\sqrt{n}(\bar x-\lambda_0)}{\sqrt{\hat \lambda}} \sim N(0,1)\]

其中, $\hat \lambda$是樣本平均值

$\chi^2$分類數據擬合度檢驗

  • 有$r$類, $A_1,A_2,\dots,A_r$
\[H_0: A_i \text{的所占的比率是} p_{i0},\quad i=1,2,\dots,r\] \[\chi^2=\sum\frac{(n_i-np_{i0})^2}{np_{i0}} \sim \chi^2(r-1)\]

列聯表的獨立性檢驗

\[H_0:p_{ij} =p_{i\cdot}p_{\cdot j} \quad i=1,\dots,r,j=1,2,\dots,c\] \[\chi^2=\sum\sum\frac{(n_{ij}-n\hat p_{ij})^2}{n\hat p_{ij}} \sim \chi^2((r-1)(c-1))\]
  • 拒絕域$W={\chi^2\geq \chi^2_{1-\alpha}((r-1)(c-1))}$

正態分布

線性迴歸和邏輯迴歸

  • 百度百科
  • 知乎參考
  • 一些例子

  • 線性回歸

  • 多重線性識別方法：VIF、散點圖和相關係數矩陣

  • 多元線性迴歸中容易出現的問題是 正態分佈問題、異方差問題、異常值問題和共線性問題

  • DW檢測：誤差項自相關或(序列相關)

抽樣

  • reference
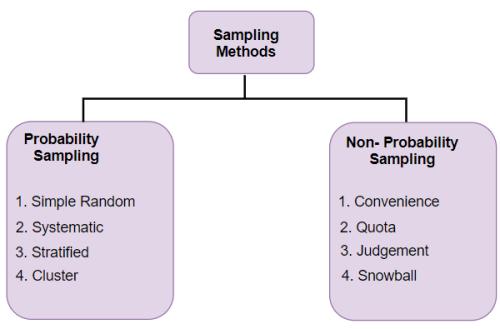
  • 分類:
    • 概率抽樣包括有簡單隨機抽樣、系統抽樣（等距抽樣）、分層抽樣（類型抽樣）、整羣抽樣

簡單隨機抽樣(simple random sampling)

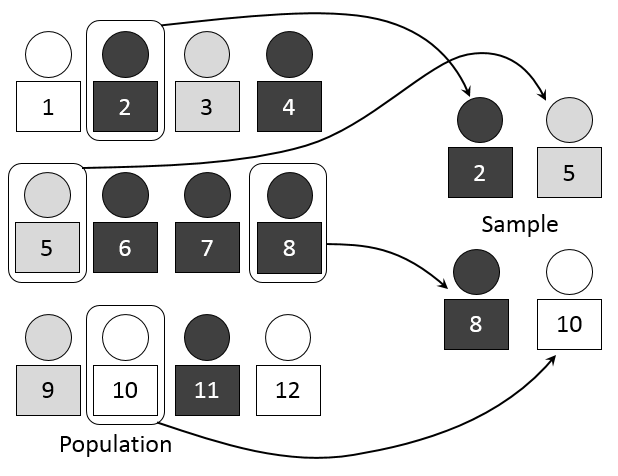
在進行抽樣時不摻入任何人為因素。母體的每一個體都有同等的機會被選中，且每次抽選與此次之前的歷次抽選無關。在進行此方法時，通常將所觀察的母體內每一個體，加以編號$1-N$，接著隨機地從這$N$個號碼中抽出我們想要的$n$個號碼(即預定的樣本數)。其次找出母體號碼中與這$n$個隨機號碼相同的個體, 這就是選出的樣本。

分層抽樣(stratified sampling)

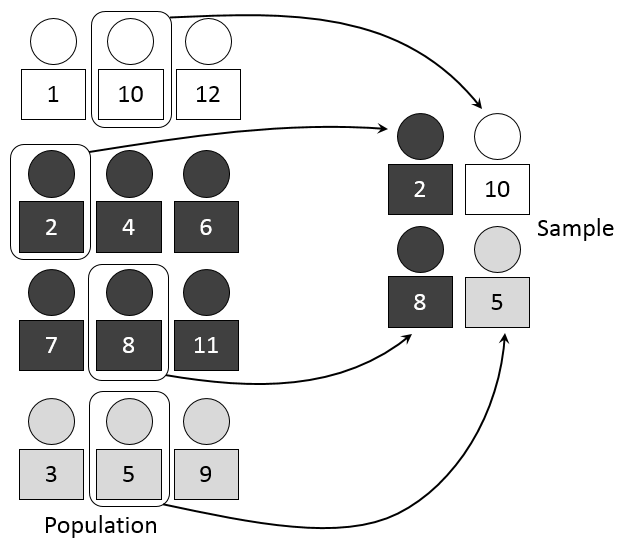
調查的母體，可依某衡量標準，區分成若干個不重複的子母體，我們稱之為『層』，且層與層之間有很大的變異性，層內的變異性較小。在區分不同層後，再從每一層中利用簡單隨機抽樣抽出所須比例的樣本數，將所得各層樣本合起來即為樣本。此處的比例就是該層的個體總數佔母體的比例。

系統抽樣(systematic sampling)

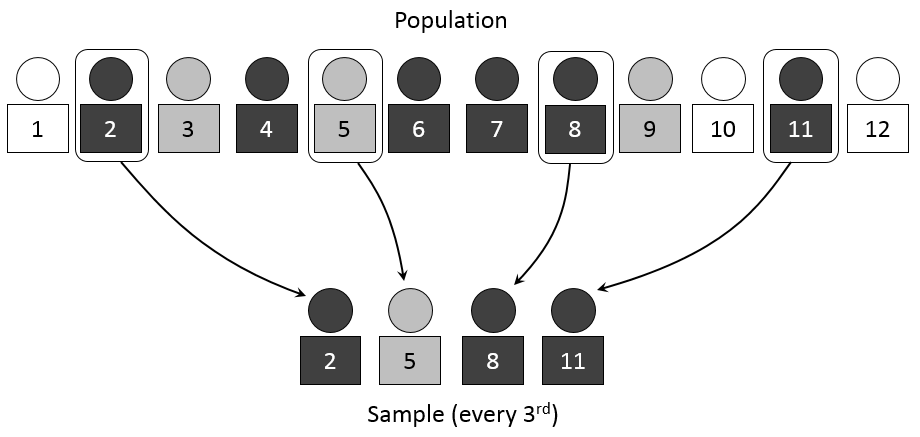
系統抽樣基本上是隻做一次簡單隨機抽樣後，就採取依固定間隔數抽出一樣本。一般而言，若母體為有限，可將母體依序編號$1,2,\cdots,N$，假設欲選取$n$個樣本，先決定區間間隔$k$，然後以簡單隨機抽樣從$1,2,\cdots,k$中選取一數，此數做為起點，依序每$k$個單位選取一樣本。通常k取為最接近$N/n$的整數。

羣集抽樣(cluster sampling)

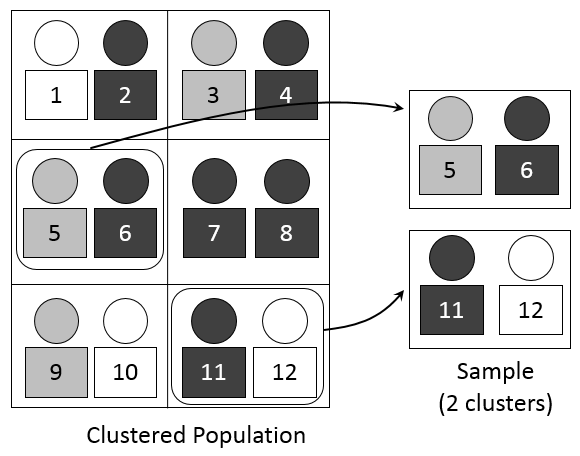
當母體的底冊的蒐集及編造極為困難或龐大，而在調查時又希望節省成本時，可採用此種抽樣。羣集抽樣的方法就是將母體分成幾個羣集(或部落、區域)，而羣集間的變異小，羣集內的變異大。再從這幾個羣集中抽出數個羣集進行抽樣或普查。有時羣集抽樣又稱部落抽樣、叢聚抽樣。

最大似然

  • 估計算
    • 無偏性、有效性、一致性 邏輯迴歸中常用的篩選變量的方法有
  • Wald test : 共線性時Wald檢驗不再有效
  • 一個似然比檢驗


數據清理和檢查

  • 隨機森林填充缺失值 對於一個有n個特徵的數據來說，其中特徵T有缺失值，我們就把特徵T當作標籤，其他的n-1個特徵和原本的標籤組成新的特徵矩陣。那對於T來說，它沒有缺失的部分，就是我們的Y_test，這部分數據既有標籤也有特徵，而它缺失的部 分，只有特徵沒有標籤，就是我們需要預測的部分。
    • 特徵T不缺失的值對應的其他n-1個特徵 + 本來的標籤：X_train
    • 特徵T不缺失的值：Y_train
    • 特徵T缺失的值對應的其他n-1個特徵 + 本來的標籤：X_test
    • 特徵T缺失的值：未知，我們需要預測的Y_test、
  • 識別異常值
  • 數據標準化

  • 聚類法

  • 錯誤值（Wrong Value）的處理是在知識發掘處理的數據清洗階段。
  • 連續變量的缺失值佔比在85%左右時，根據是否缺失，生成指示變量，僅使用指示變量作爲解釋變量
  • 标准化之后，利用正负3倍标准差识别异常值


主成分分析、因子分析、對應分析等

主成份分析(PCA)

  • 變化過後的新的特徵，兩兩之間完全獨立
  • 新的特徵的方差就是其所對應的特徵值
  • 做PCA最好需要做標準化
  • 主成分分析關注變量之間的相關關係
  • 因子分析關注維度的含義
  • 對應分析關注行變量和列變量兩者的相關性。
  • 多維尺度分析關注行變量之間的相似性

對應分析

  • 對應分析用於兩個離散型變量之間的分析
  • 能夠分析變量（列）與樣本（行）之間的關係
  • 夠分析樣本（行）與樣本（行）之間的關係## 時間序列
  • 兩個向量的長度越長，且夾角越小，那麼對應性越強

相關分析

  • 數據間相互獨立，包括觀測間相互獨立與變量間相互獨立
  • 兩列變量均服從正態分佈
  • 變量爲連續變量
  • 兩變量間的關係是線性的

You May Also Enjoy