脈波調變
Published:
參考
- 這是閱讀書本<通訊原理與應用>,作者藍國桐。
定義
- 在以下的過程當中,假設調變信號$s(t)$是
\begin{equation} \label{signal} s(t)=A_m \cos(2\pi f_m t), \end{equation}
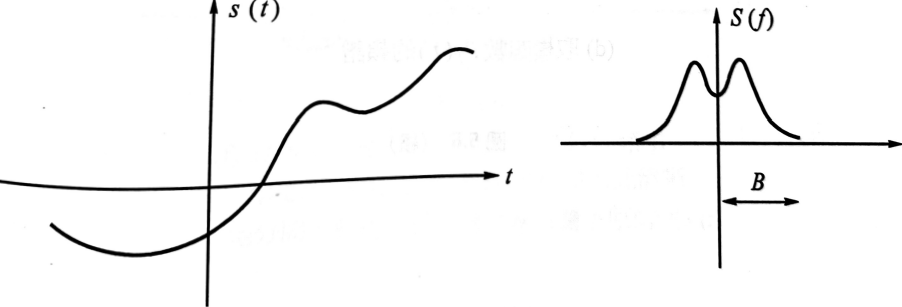
雖然是這樣定義,但經Fourier Series,任何週期波都可以表達成$\eqref{signal}$的和。它的Fourier Transform, 稱為頻譜或$S(t)=\mathcal{F}(s(t))$
- 在調變後的結果會以$\phi(t)$表示, 它的Fourier Transform, 稱為頻譜或$\Phi(t)=\mathcal{F}(\phi(t))$
- 解調後的信號會以$s_0(t)$表示
取樣程序
理論上可利用$\delta (t-nT_s)$
\begin{equation}\label{ins_sampling} s_{\text(int)}=\sum_{n=-\infty}^{\infty}s(t)\delta(t-nT_s) \end{equation}
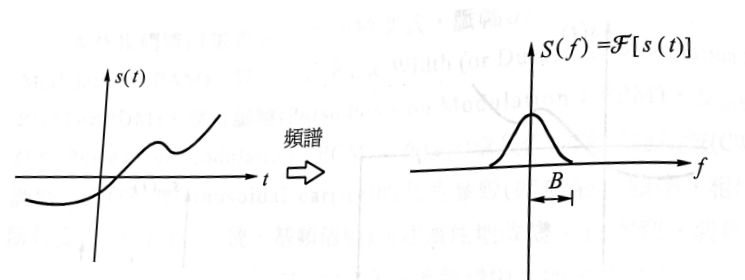
- 它的頻譜
\begin{equation}\label{ins_sampling_ft} S_{\text(int)}(f)=\mathcal{F}(s_{\text(int)})=f_s\sum_{n=-\infty}^{\infty}S(f-nf_s) \end{equation}
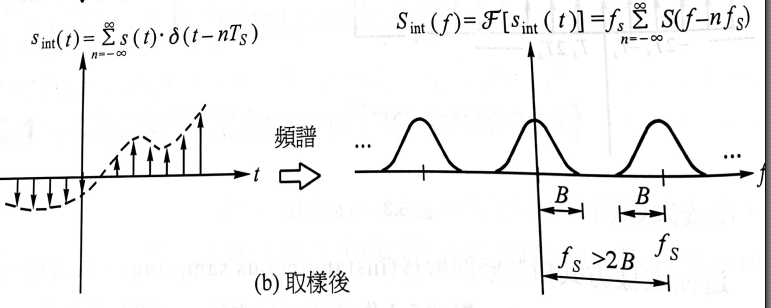
實際上可利用$p_T (t-nT_s)$
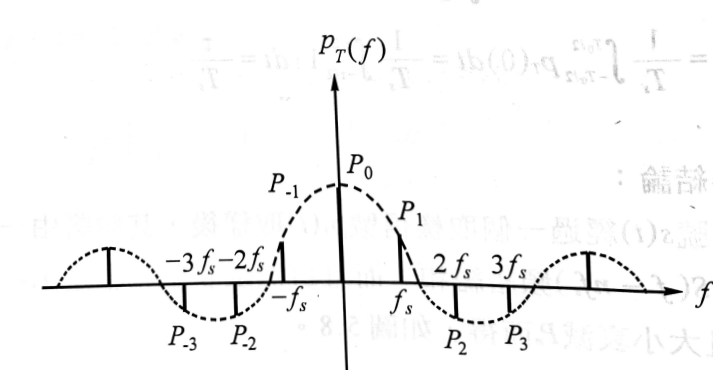
\begin{equation} \label{pT_fs} p_T(t)=\sum_{n=-\infty}^{\infty}P_n e^{jn2\pi f_s t} \end{equation}
其中
\[P_n=\frac{1}{T}\int_{\frac{-T_s}{2}}^{\frac{T_s}{2}}e^{-jn2\pi f_s t}dt=\frac{1}{n\pi}\sin(n\pi f_s\tau)=f_s\tau \frac{\sin(n\pi f_s \tau)}{n\pi f_s \tau}\]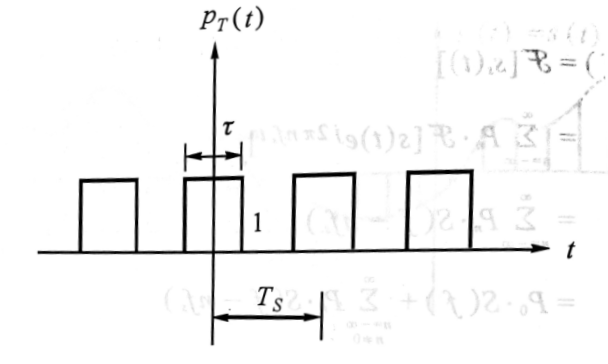
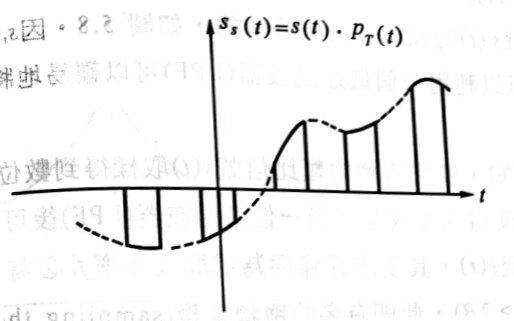
- 原信號$s(t)$取樣後$s_s(t)$為
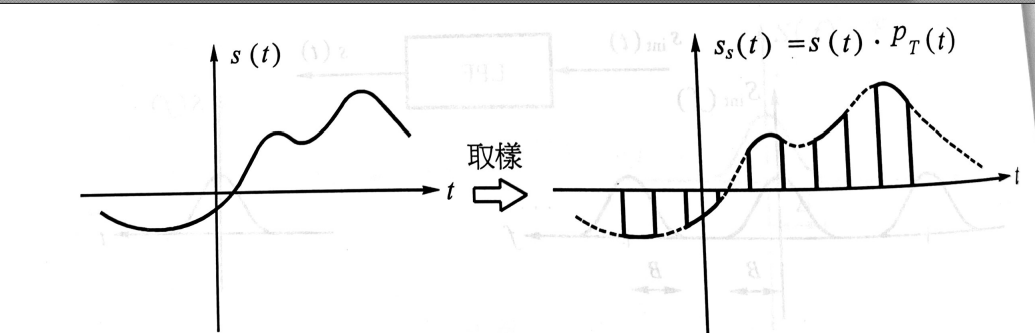
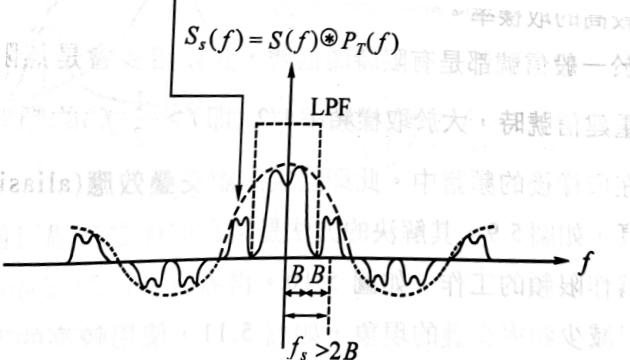
- $s_s(t)$的頻譜$S_s(f)$
其中$P_0=\frac{\tau}{T_s}$
取樣定理
以$s(t)$代表一頻寬有限的信號,並以$f_m$代表頻寬。如果隔$T_s$移取樣一次,只要
\[f_s>2f_m\]就能從$s(nT_s)$取回原來的信號而不失真。
PAM
平頂式取樣
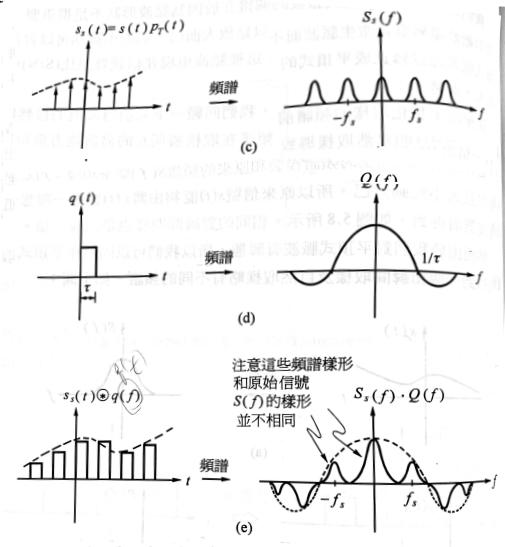
圖 1
- 因為脈波形狀不是很重要, 所以可以用平頂式取樣
- 中繼站能重新產生脈波或修正成平頂式,這使重現存在雜訊的信息有很大優勢
- 它的數學式為$s_s(t)*q(t)$
- 它的頻譜為$S_s(f)Q(f))$, 比較$S_s(f)$, 已扭曲
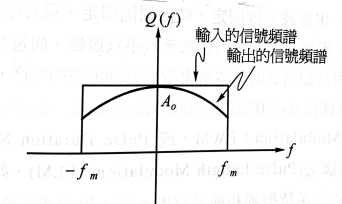
圖 2:某通道對脈波信號的頻率響應
- 所以要得到$s_s(t)$的頻譜$S_s(f)$, 必須將$S_s(f)Q(f))$乘以$Q^{-1}(f)$用來校正,這個校正系統叫作等化器
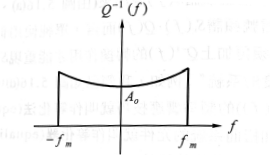
圖 3:中繼站還原用的等化器
PCM
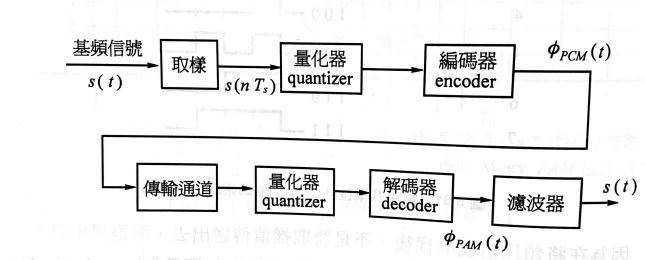
圖 4:PCM過程
- 基頻信號經過取樣、量化和編三個程序, 稱為A/D轉換。
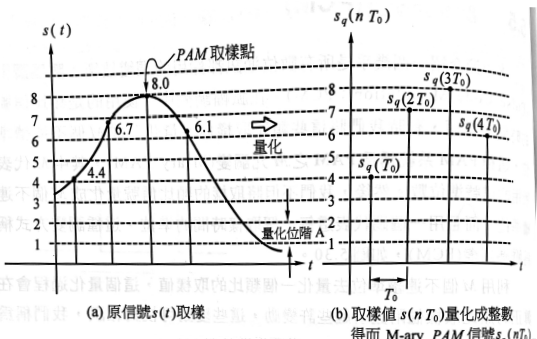
圖 5:取樣和量化
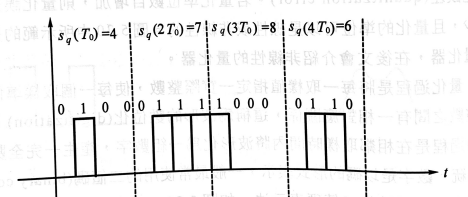
圖 6:編碼
- 量化過程可能對振幅少的信號不利, 會使用壓縮器, 使振幅不大的部分擴大振幅, 而振幅大的不再擴大。而在接收端需要和壓縮器完全相反的伸張器
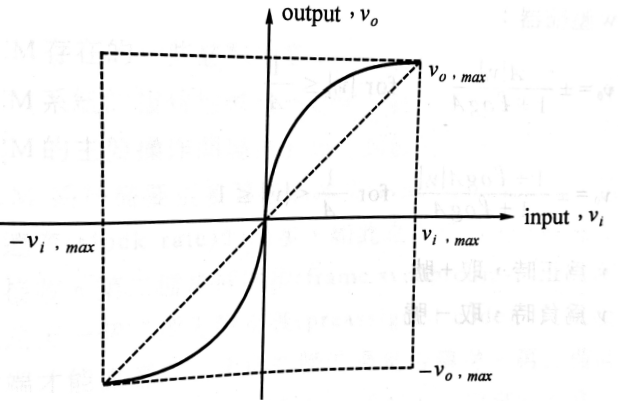
圖 6:編碼
- $\phi_{PCM}(t)$必須先經過量化器再加以解碼, 因為藉由量化可以消除因傳輸通道而得到的雜訊
- 解碼後可得到PAM信號, 再濾波器對PAM信號作平滑化動作之後可得基頻信號$s(t)$
優點
- 能在中繼站再生信號
- 調變和解調電路都是數位,高可靠和穩定
- 可用有效的編碼方式
- 編碼可減少雜訊和干擾
- 價格低、容易多工、容易交換和低雜訊處理
缺點
- PCM系統複雜性較其他系統來的高
- 主要操作問題是類比和數位的轉換
- PCM系統需要很多等級的同步
- 時脈(CLOCK RATE)的同步
- 框(FRAME SYNCHRONIZATION)同步
- 比類比調数需要更大的頻寬
