Elsa CHOI

Elsa CHOI

振幅調變

1 minute read

Published:

參考

定義

  • 在以下的過程當中，假設調變信號$s(t)$是

\begin{equation} \label{signal} s(t)=A_m \cos(2\pi f_m t), \end{equation}

雖然是這樣定義，但經Fourier Series，任何週期波都可以表達成$\eqref{signal}$的和。它的Fourier Transform, 稱為頻譜或$S(t)=\mathcal{F}(s(t))$

  • 在調變後的結果會以$\phi(t)$表示, 它的Fourier Transform, 稱為頻譜或$\Phi(t)=\mathcal{F}(\phi(t))$
  • 解調後的信號會以$s_0(t)$表示

DSB-LC


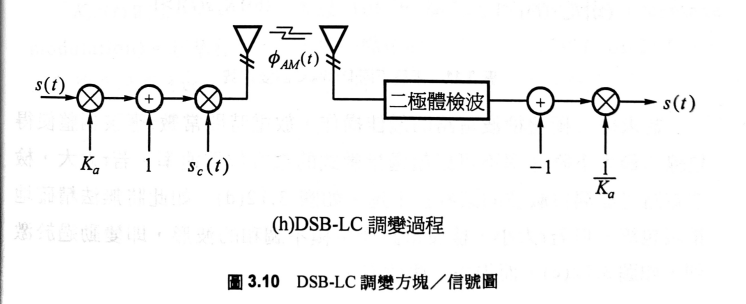
圖 1:DSB-LC過程

調變

  • 以下是載波$\phi_{AM}(t)$

\begin{equation} \label{am1} \phi_{AM}(t)=A_c[1+K_a s(t)]cos(2\pi f_c t)\quad \text{where }fc \gg f_m \text{ and }|K_a s(t)|<1 \end{equation}

  • $\phi_{AM}(t)$的頻譜

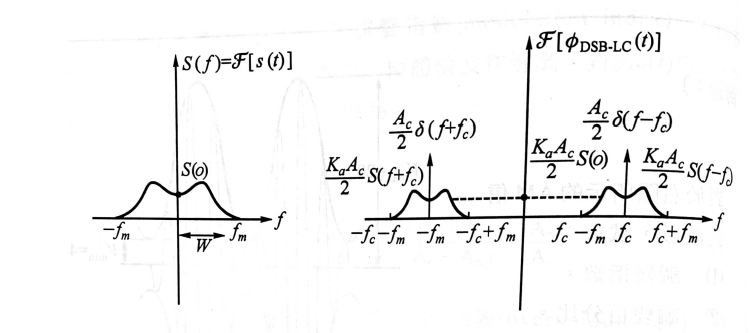
圖 2:$\phi_{AM}(t)$的頻譜
  • 調變百分比$m$
\[\begin{align} m &=K_a A_m \label{m_index_1}\\ \text{and by } \eqref{am1} \quad \frac{\phi_{\max}}{\phi_{\min}}&=\frac{A_c(1+m)}{A_c(1-m)} \\ m&=\frac{\phi_{\max}+\phi_{\min}}{\phi_{\max}-\phi_{\min}} \label{m_index_2} \end{align}\]
  • AM總功率$P$、載波功率$P_C$和上旁波帶功率$P_{USB}$
\[P=P_C+P_{USB}+P_{LSB}=P_C+\frac{m^2}{4} P_C+\frac{m^2}{4} P_C=(1+\frac{m^2}{2})P_C\]

調解

  • 用二極體和R-C電壓去檢測載波$(1+K_a)s(t)$的包線,即是$s(t)$

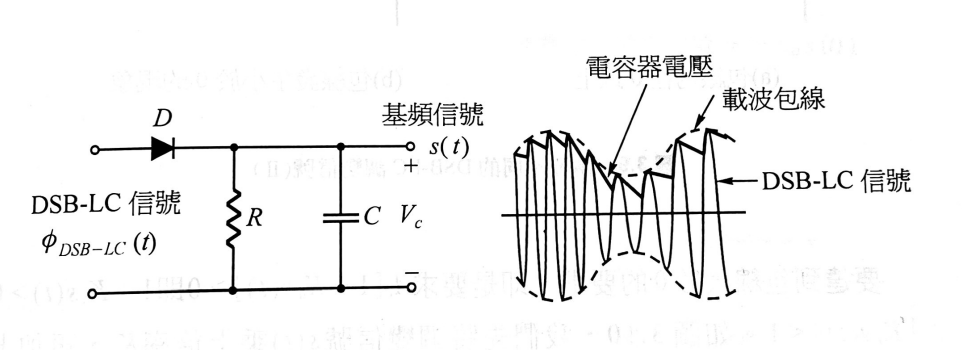
圖 3:檢測載波的包線

優點

  1. 解調電路簡單

缺點

  1. 欲傳達的訊息包含在旁波帶之內$P_{USB}+P_{LSB}$, AM信號的功率卻集中在載波$P_C$, 形同功率的浪費
  2. 頻寛是$2f_m$

DSB-SC


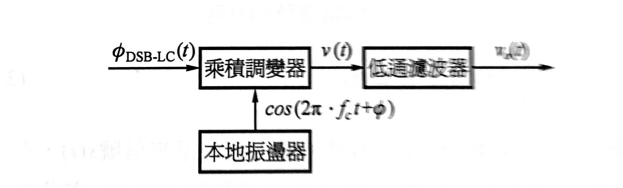
圖 4: DSB-SC過程
  • 調變：載波$\phi_{DSB-SC}(t)$

\begin{equation} \label{shift1} \phi_{DSB-SC}(t)=s(t)\cos(2\pi f_c t) \end{equation}

  • 載波$\phi_{DSB-SC}(t)$的頻譜會以$f_c,-f_c$為中心, 向左向右平移$f_m$,頻譜強度變為0.5, 表達式為以下

\begin{equation} \label{ft_shift1} \Phi(f)=\frac{1}{2}(S(f-f_c)+f(f+f_c)) \end{equation}


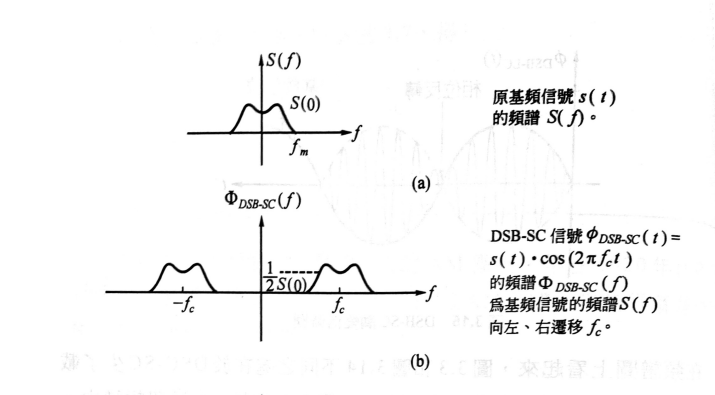
圖 5.1: $\phi_{DSB-SC}(t)$的頻譜

解調

  • $\phi_{DSB-SC}(t)$乘以$\cos(2\pi f_c t)$得以下
\[\phi_{DSB-SC}(t)\cos(2\pi f_c t)=\frac{1}{2}(s(t)+\cos(4\pi f_c t))\]
  • $\phi_{DSB-SC}(t)$的頻譜：
    • 以$2f_c,-2f_c$為中心, 向左向右平移$f_m$, 大小為原來的$\frac{1}{4}$
    • 以$0$為中心, 向左向右平移$f_m$, 大小為原來的$\frac{1}{2}$。這個剛好是原頻譜的$\frac{1}{2}$倍

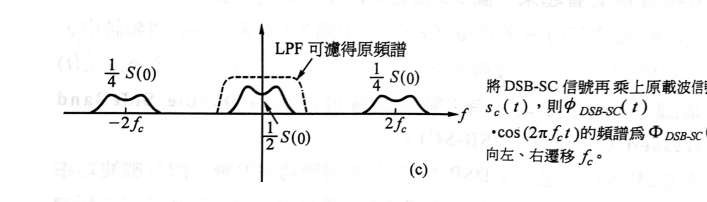
圖 5.2: $\phi_{DSB-SC}(t)\cos(2\pi f_c t)$的頻譜
  • 因為$2f_c$是比較高頻的, 先過濾, 就會得到原頻譜的$\frac{1}{2}$倍

優點

  • DSB-SC比起DSB-LC減少載波功率的浪費

缺點

  • 頻寬為$2f_{m}$,但因為$s(t)$是實數, 所以對於$f=0$對稱
  • 當解調器的相位$\phi$, 即$\phi_{DSB-SC}(t)$解調時乘以$\cos(2\pi f_c t+\phi)$, 再濾高頻,會得
\[s_0(t)=\frac{1}{2}s(t)\cos(\phi)\]

從上式可見, 當$\phi=0$時, $s_0(t)=0$,稱為同調波器的正交空效應

  • 若解調器的振𣿴器的頻率$f_c’$,它與$f_c$的差為$\Delta f$, 那麽用上述方法解調出來的$s_0(t)$會是
\[s_0(t)=\frac{1}{2}s(t)\cos(2\pi \Delta f t)\]

從上式可見, $s_0(t)$會有失真, 通常$\Delta f\leq 30\text{HZ}$是可以接受的

  • 綜合可見，這個DSB-SC需要更複雜的同步解調系統
\[s_0(t)=\frac{1}{2}s(t)\cos(2\pi \Delta f t+\Delta \theta)\]

DSB-SSB

調變

  • 取DSB-SC頻譜$\Phi_{DSB-SC} (f)$中,$f> f_c$的上旁波帶
\[\phi_{SSB}(t)=\frac{1}{2}(s(t)\cos(2\pi f_ct))-\hat s(t)\sin(2\pi f_ct))\]

其中$\hat s(t)$是$\mathcal{F}^{-1}(\hat S(f))$ ,$S(f)=-\text{sign}(f)j S(f)$

  • \(\Phi_{SSB}(f)\)的頻譜是以$f_c$為中心, 向右平移$f_m$, 大小為原來的$\frac{1}{4}$, 再與$f=0$對稱得到$-f_c$的部分

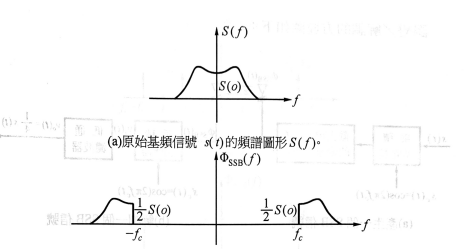
圖 5: $\phi_{DSB-SC}(t)$ 上旁波帶

解調

  • 乘以$\cos(2\pi f_ct)$
\[\phi_{SSB}(t)\cos(2\pi f_ct))=\frac{1}{2}(0.5s(t)(1+\cos(2\pi f_c t))-0.5\hat s(t)\sin(2\pi f_c t))\]
  • 過濾高頻$2f_c$,得到以下
\[s_0(t)=\frac{1}{4}s(t)\]

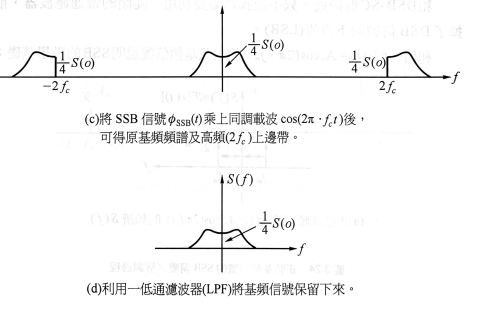
圖 5: $\phi_{SSB}(t)$ 解頻

優點

  • 只用$f_m$頻寬

缺點

  • 同DSB-SC一樣定義$\Delta f , \Delta \theta$,假如$s(t)=A_m\cos(2\pi f_m t)$,那麽調解出來的$s_0(t)$
\[s_0(t)=\frac{1}{4}A_m\cos(2\pi (f_m-\Delta f) t-\Delta \theta)\]
  • 在DSB-SC, $\Delta \theta \neq 0,\Delta f=0$只會導致振幅衰減, 但是SSB會導致相角的偏差而導致失真, 所以在影像資料就不能使用,但可用在語音通訊
  • 當$\Delta \theta =0 ,\Delta f\neq 0$,
\[\cos(2\pi (f_m-\Delta f) t-\Delta \theta)=\cos(2\pi (f_m) t)\cos(2\pi (\Delta f) t)\]

若$\Delta f \ \propto f_m$,這只是音調較高或較低,這失真引起老鴨反應。

You May Also Enjoy