Elsa CHOI

Elsa CHOI

CT Fourier Transform

3 minute read

Published:

Sources

Unit impulse signal

Roughly,we can recognize unit impulse as 1 at 0 , 0 otherwise.

$\delta(t)$ has the following properties:

  • $\int_{-\infty}^{\infty}x(t)\delta(t)dt=x(0)=\frac{x(0^{+})+x(0^{-})}{2}$
  • $\int_{-\infty}^{\infty} \delta(t) dt=1$
  • $\delta(t)=0 \quad \forall t\neq 0$
  • $z(t)\delta(t)=z(0)\delta(t)$
  • $\int_{-\infty}^{\infty} x(t) \delta(t-t_0)=x(t_0)$
  • $\int_{-\infty}^{\infty} x(t) \delta(at)=\frac{1}{ \vert a\vert }x(0) \quad \forall a \neq 0$
  • $\delta(at)=\frac{1}{ \vert a\vert }\delta(t) \quad \forall a \neq 0$
  • $\int_{-\infty}^{\infty}\delta(\tau) \delta(t-\tau)d\tau=\delta(t)$
  • $\delta(t)=\int_{-\infty}^{\infty} e^{jt\omega} d\omega$

Unit-step function

Roughly, we can recognize unit-step impulse as $u(t)=1 \quad t\leq 0$ , 0 otherwise.

  • $u(t)=\int_{0}^{\infty}\delta(t-\tau)d\tau$
  • $u(t)=\int_{0}^{\infty}\delta(t-\tau)d\tau=\int_{0}^{\infty}u(\tau)\delta(t-\tau)d\tau=\int_{0}^{\infty}u(t-\tau)\delta(\tau)d\tau$

CT Fourier Transform

If $x(t)$ is $T_0$-periodic, $x(t)$ can be written as

\begin{equation} \label{Fourier1} x(t)=\sum\limits_{k=-\infty}^{\infty}X_k e^{jk\omega_0 t} \end{equation}

\begin{equation} \label{Fourier2} X_k=\frac{1}{T_0}\int_{-\frac{T_0}{2} }^{\frac{T_0}{2}}x(t) e^{-jk\omega_0 t}dt \end{equation}

Define the complex-valued function $X(\omega)$ by

\begin{equation} \label{def_X} X(\omega)=\int_{-\frac{T_0}{2} }^{\frac{T_0}{2}}x(t) e^{-j\omega t}dt \end{equation}

Hence,

\begin{equation} \label{Fourier3} X_k=\frac{1}{T_0}X(k\omega_0)=\frac{\omega_0}{2\pi}X(k\omega_0) \end{equation}

\begin{equation}\label{Fourier4} x(t)=\sum\limits_{k=-\infty}^{\infty} \frac{\omega_0}{2\pi}X(k\omega_0)e^{jk\omega_0 t} \end{equation}

Considering $T_0 \rightarrow \infty$, that is, $\omega_0 \rightarrow 0$

\begin{equation}\label{Fourier5} x(t)=\sum\limits_{k=-\infty}^{\infty} \frac{\omega_0}{2\pi}X(k\omega_0)e^{jk\omega_0 t} =\frac{1}{2\pi}\int_{-\infty }^{\infty}X(\omega) e^{jk\omega t}d\omega \end{equation}

and $\eqref{def_X}$ becomes

\begin{equation}\label{Fourier6} X(\omega)=\int_{-\infty}^{\infty}x(t) e^{-jk\omega_0 t}dt \end{equation}

$X(\omega)$ meaning

In fact, the Fourier transform $X(\omega)$ describes the frequency content of the signal $x(t)$. Usually using the magnitude spectrum and the phase spectrum to show.

Example:

\[x(t)=e^{-3t}u(t)\]

According $\eqref{Fourier6}$,

\[\begin{aligned} X(\omega) &=\int_{-\infty}^{\infty}x(t) e^{-j\omega_0 t}dt \\ &=\int_{0}^{\infty}e^{-3t} e^{-j\omega_0 t}dt \\ &=\frac{-1}{3+j\omega}e^{-(3+j\omega)t}\Bigg\vert_{0}^{\infty} \\ &=\frac{1}{3+j\omega} \end{aligned}\]

Hence,

\[\vert X(\omega)\vert =\frac{1}{\sqrt{9+\omega^2}}\]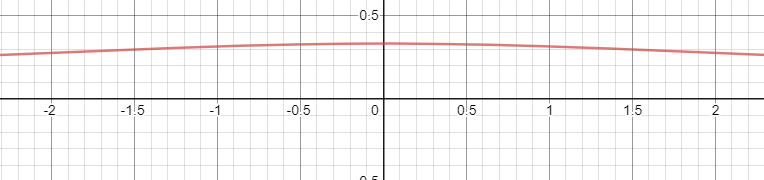

圖 1
\[\text{phase}(X(\omega) )=\tan^{-2}(\frac{\omega}{3})\]

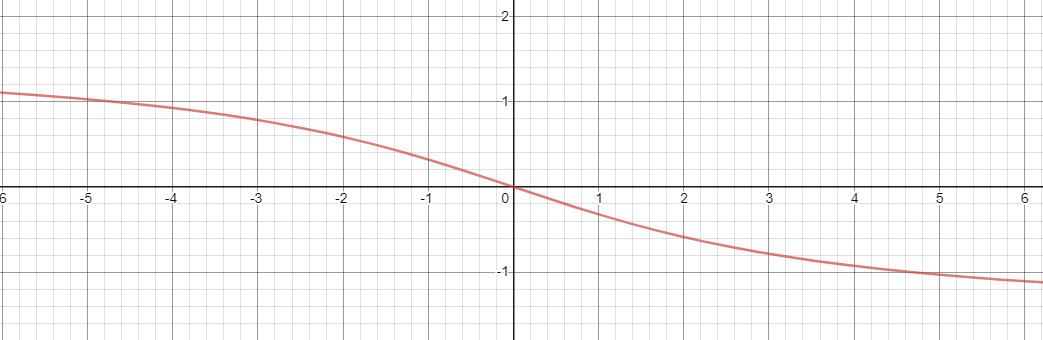
圖 2

Remark:by $\eqref{Fourier6}$

\[X^{*}(\omega)=(\int_{-\infty}^{\infty}x(t) e^{-jk\omega_0 t}dt)^*=\int_{-\infty}^{\infty}x(t) e^{jk\omega_0 t}dt=X(-\omega)\]

Examples:

  1. $x(t)=\delta(t)$, by shifting property
\[X(\omega)=1\]
  1. \[x(t)=\Bigg\{ \begin{aligned} &1 \quad &t \in [-T_1,T_1] \\ &0 \quad &\text{otherwise} \end{aligned}\]

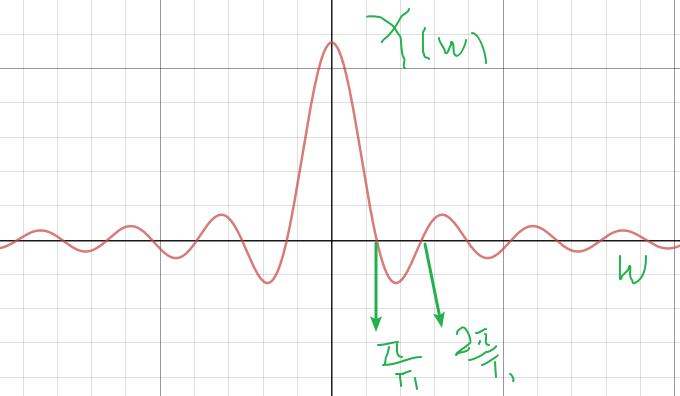
圖 3
\[\begin{aligned} X(\omega)&=\int_{-T_1}^{T_1}e^{(-j\omega t) }dt=\frac{1}{j\omega}(e^{j\omega T_1}-e^{-j\omega T_1})\\ &=2T_1\frac{1}{\omega T_1}\sin(\omega T_1)=2T_1\text{sinc}(\frac{\omega T_1}{\pi}) \end{aligned}\]

Fourier Transform for periodic signals

If $x(t)$ is $T_0$-periodic, then its Fourier transform is

\[X(\omega)=\int_{-\infty}^{\infty}x(t)e^{-j\omega t} dt\]

which is not exist in the general cases. However, if we consider Fourier series expression $x(t)$, which is

\[x(t)=\sum_{k=-\infty}^{\infty}X_k e^{jk\omega_0 t}\]

and look at the fact that when $x(t)=e^{j\omega_0 t}$, its Fourier transformation $X(\omega)$

\[X(\omega)=\int_{-\infty}^{\infty}e^{j\omega_0 t}e^{-j\omega t} dt =2\pi\delta(\omega_0-\omega)=2\pi\delta(\omega-\omega_0)\]

Therefore, it is reasonable to consider

\[\begin{align} X(\omega) &=\int_{-\infty}^{\infty}x(t)e^{-j\omega t}dt \\ &=\int_{-\infty}^{\infty}\sum_{k=-\infty}^{\infty}X_k e^{jk\omega_0 t} e^{-j\omega t} dt \\ &=\sum_{k=-\infty}^{\infty}X_k \int_{-\infty}^{\infty}e^{jk\omega_0 t}e^{-j\omega t} dt \\ &=\sum_{k=-\infty}^{\infty}2\pi X_k\delta(\omega-k\omega_0) \label{FourierSeries_X} \end{align}\]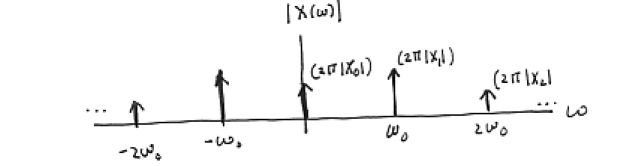

圖 4

Example:

\[x(t)=\sum_{k=-\infty}^{\infty}\delta(t-k)\]

We directly compute $X(\omega)$ as following:

\[\begin{aligned} X(\omega)&=\int_{-\infty}^{\infty}\sum_{k=-\infty}^{\infty}\delta(t-k)e^{-j\omega t}dt \\ &=\sum_{k=-\infty}^{\infty}\int_{-\infty}^{\infty}\delta(t-k)e^{-j\omega t}dt \\ &=\sum_{k=-\infty}^{\infty}e^{-j\omega k} \end{aligned}\]

Other approaches is to get the Fourier Series Data of $x(t)$. First, observing that $x(t)$ has period $1$, which implies $\omega_0=2\pi$.

According $\eqref{Fourier2}$,

\[\begin{aligned} X_n&=\int_{-1/2}^{1/2} \sum_{k=-\infty}^{\infty} \delta(t-k) e^{-j n \omega t} dt\\ &=\int_{-1/2}^{1/2} \delta(t) e^{-j n \omega t} dt \quad \text{ (since only }\delta(t-0)\text{ has nonzero value in [-1/2,1/2] )} \\ &=\int_{-\infty}^{\infty} \delta(t) e^{-j n \omega t} dt \\ &=e^{-j n \omega 0}=1 \end{aligned}\]

Finally, the Fourier seriers data of $x(t)$ is

\[x(t)=\sum_{k=-\infty}^{\infty}e^{-jk2\pi t}\]

We have compute the Fourier transform of Fourier series in general, so by $\eqref{FourierSeries_X}$,

\[X(\omega)=\sum_{k=-\infty}^{\infty}2\pi\delta(\omega-k2\pi)\]

We prefer the last method one.

Properties of the Fourier Transform

\[\begin{aligned} F(x(t))&=\int_{-\infty}^{\infty}x(t)e^{-j\omega t} dt \\ F^{-1}(X(\omega) )&=\frac{1}{2\pi}\int_{-\infty}^{\infty}X(\omega)e^{j\omega t} d\omega=x(t) \end{aligned}\]
  • Linearity
\[F(x(t)+ay(t))=X(t)+aY(t)\]
  • Time Shifting
\[F(x(t-t_0))=e^{j\omega t_0}X(\omega)\]
  • Time Scaling If $a\neq 0$
\[F(x(at))=\frac{1}{ \vert a \vert }X(\frac{\omega}{a})\]
  • Differentiation
\[F\bigg(\frac{d}{dt}x(t)\bigg)=j\omega X(\omega)\]
  • Integration
\[F\bigg(\int_{-\infty}^{t} x(\tau)d\tau \bigg)=\frac{1}{j\omega} X(\omega)+\pi X(0)\delta(\omega)\]

Example: by integration property,

\[F(u(t))=\frac{1}{jw}+\pi\delta(\omega)\]

Convolution Property and Frequency Response of LTI Systems

  • modulation / frequency shifting
\[F(e^{j\omega_0 t}x(t))=X(\omega-\omega_0)\]
  • Convolution
\[F( (x*y)(t) )=X(\omega)H(\omega)\]
  • Freqyency-Domain Convolution
\[F( x(t)y(t) )=\frac{1}{2\pi}(X*Z)(\omega)\]
  • Inverse Freqyency-Domain Convolution
\[F^{-1}( \frac{1}{2\pi}(X*Z)(\omega))=x(t)y(t)\]

Example:

\[x(t)=[1+km(t)]cos(\omega_c t)\]

where $cos(\omega_c t)$ is called carrier signal, $m(t)$ is called message signal and $k$ is called the modulation index. Assume message singal is banedlimiited by $\omega_m \ll \omega_c$


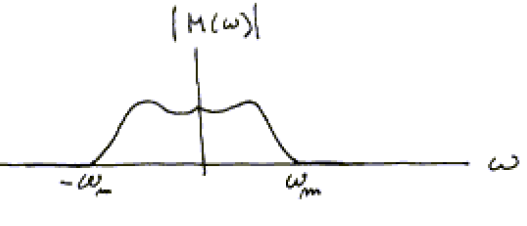
圖 5
\[F(cos(\omega_c t))=\pi(\delta(\omega-\omega_c)+\delta(\omega+\omega_c))=X(\omega)\] \[\begin{aligned} F(m(t)cos(\omega_c t)) &=\int_{-\infty}^{\infty}M(\xi)X(\omega-\xi)d\xi \\ &=\int_{-\infty}^{\infty}M(\xi)\pi(\delta(\omega-\omega_c-\xi)+\delta(\omega+\omega_c-\xi)) d\xi \\ &=\frac{1}{2}\bigg\{ M(\omega-\omega_c)+M(\omega-\omega_c) \bigg\} \end{aligned}\]

We conclude that

\[X(\omega)=\pi(\delta(\omega-\omega_c)+\delta(\omega+\omega_c))+\frac{k}{2} (M(\omega-\omega_c)+M(\omega+\omega_c))\]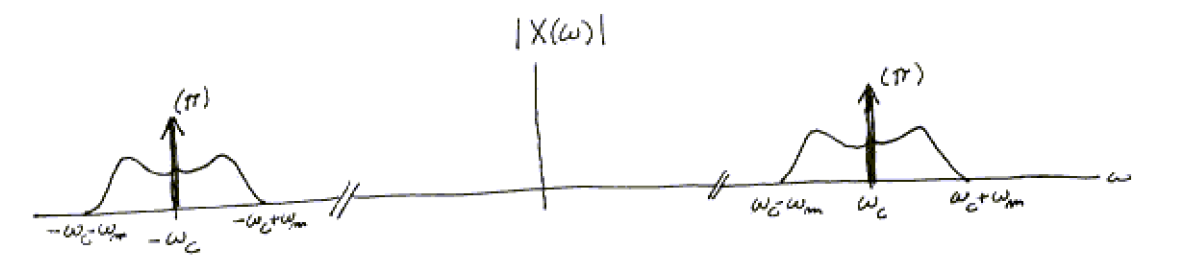

圖 6

Parseval’s Theorem

\[\int_{-\infty}^{\infty} x^2(t)dt=\frac{1}{2\pi}\int_{-\infty}^{\infty}\vert X(\omega)\vert^2 d\omega\]

Duality Property

If $x(t)$ has Fourier Transform $X(\omega)$

\[F(X(t))=2\pi x(-\omega)\]

Offical 420.214 CT Fourier Transform Table


圖 7

You May Also Enjoy