Elsa CHOI

Elsa CHOI

高中物理-電磁感應

less than 1 minute read

Published:

法拉第定律

電磁感應現象

1 、產生電磁感應的條件：
法拉第認為，當一封閉線圈內的磁力線數目 ($\Phi_B$) 發生變化時，線圈會產生感應電
動勢以反抗磁通量繼續變化。
2 、磁通量 $\Phi_B$ ：
垂直通過某任意封閉曲面之磁力線總條數 :

\begin{equation} \label{Lenz’s law} \Phi_B=B_{\bot}A=\vec{B}\cdot \vec{A}=BA\cos \theta \quad (\text{unit:wb}) \end{equation}

冷次定律


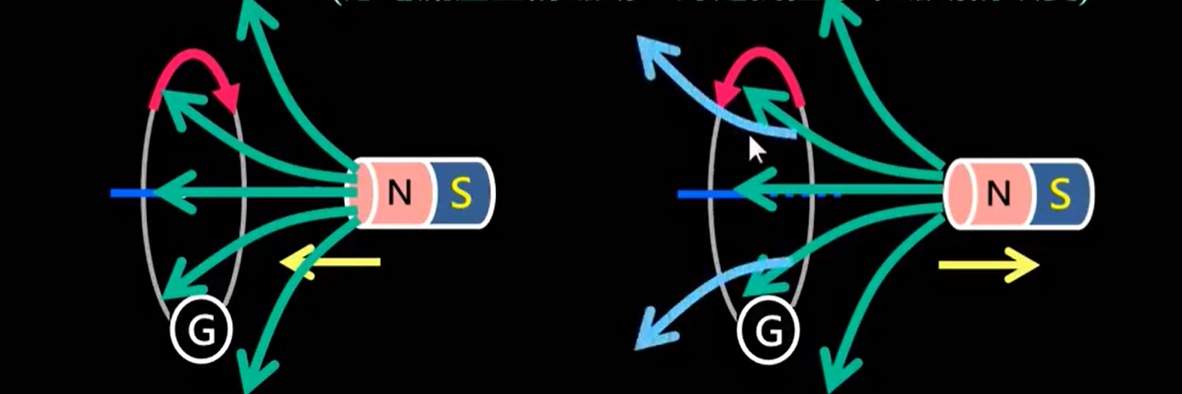
圖 1

圖 2
  1. 用途：判斷感應電流方向
  2. 方法：感應電流的方向是為了反抗磁通量$\Phi_B$的變化。

法拉第定律


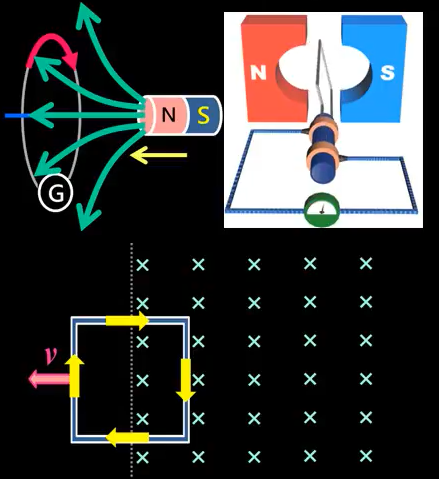
圖 3
  1. 封閉線圈內有磁通量變化時，會產生感應電動勢以反抗磁通量繼續變化
  2. 短導線有切割磁力線
\[\begin{align} \label{Faraday's law} \varepsilon_av&=-N\frac{\Delta \Phi_{B}}{\Delta t} \\ \varepsilon_t&=-N\frac{d\Phi_{B}}{ dt} \end{align}\]

其中，磁通量数化類形： \(\begin{aligned} \Delta \Phi_B&=\Delta B \cdot A \\ \Delta \Phi_B&= B \cdot \Delta A \end{aligned}\)

法拉第定律-短導線切割磁力


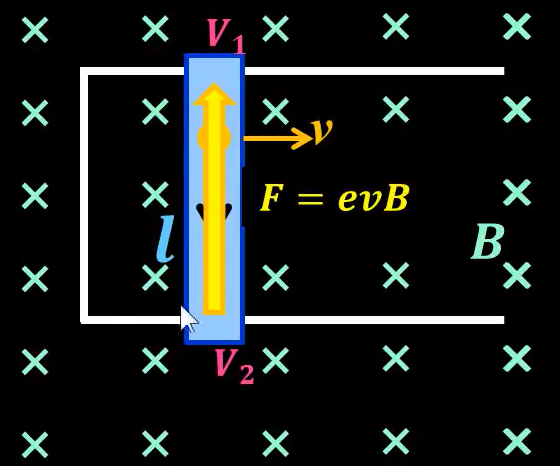
圖 4
\[\begin{aligned} \varepsilon_av&=-N\frac{\Delta \Phi_{B}}{\Delta t} \\ &=-N\frac{B \cdot \Delta A}{\Delta t}\\ &=-N\frac{B \cdot lv\Delta t}{\Delta t}\\ &=-NlvB \end{aligned}\]

由載流導線在磁場中所受的磁力得知, 磁力$F$作功

\[W=Fl=qvBl\]

會轉化為電位能

\[qvBl=q(V_2-V_1) \implies V_2-V_1=vBl\]

發電機


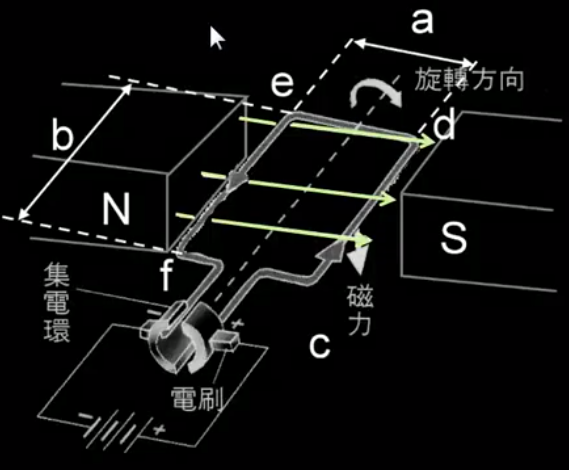
圖 5:電動機
 原理公式
電動機電動生磁$NBAi \sin \theta$
發電機磁動生電$NBA\omega \sin \omega t$

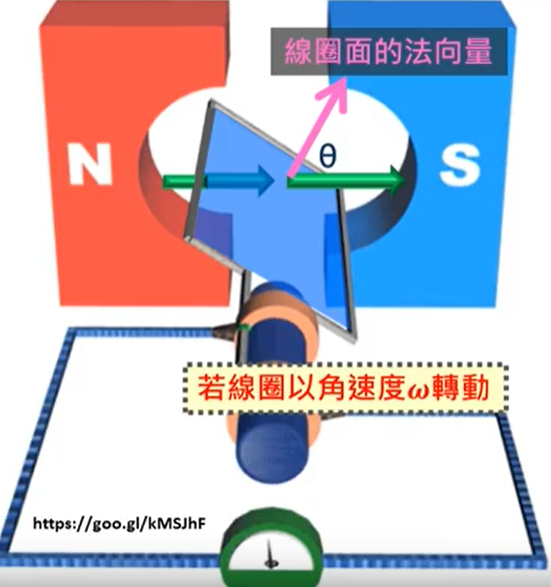
圖 6:發電機

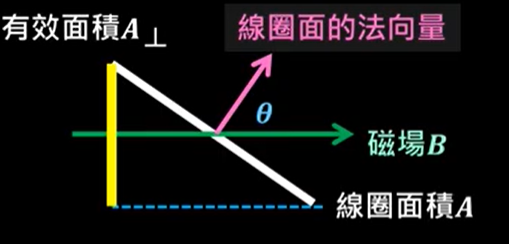
圖 7:發電機
  • 磁通量$\Phi_B$:
\[\begin{aligned} \Phi_B=BA\cos\theta=BA\cos \omega t \end{aligned}\]
  • 瞬間電動勢$\varepsilon$:
\[\begin{aligned} \varepsilon&= -N\frac{d\Phi_B}{dt}\\ &=-NBA\frac{d(\cos \omega t)}{dt}\\ &=-NBA(-\omega \sin \omega t)\\ &=NBA\omega \sin \omega t \end{aligned}\]

變壓器

  1. 結構：將兩組匝數不同的線圈，纏繞於同一軟鐵心上所製成，輸入電流的線圈稱為主線圈輸出電流的線圈稱為副線圈。
  2. 原理：主線圈與交流電連接，利用交流電產生變化的磁通量，此變化的磁通量透過軟鐵心傳到副線圈處，並在副線圈上感應出交流電壓。
  3. 使用限制：限用於交流電源 ( 變壓前後頻率不變 )
  4. 公式：
\[\begin{aligned} \varepsilon&= -N\frac{d\Phi_B}{dt}\\ \implies \frac{\varepsilon_1}{\varepsilon_2} &=\frac{-N_1\frac{d\Phi_B}{dt}}{-N_2\frac{d\Phi_B}{dt}}\\ \implies \frac{\varepsilon_1}{\varepsilon_2}&=\frac{N_1}{N_2} \end{aligned}\]

理想變壓器轉換過程無耗能：

\[P_{text{in}}=P_{\text{out}} \implies i_1V_1=i_2V_2\]

其中， $P=i^2R=\frac{V^2}{R}$

You May Also Enjoy