Elsa CHOI

Elsa CHOI

高中物理-電流磁效應

2 minute read

Published:

簡介

  • 這是複習高中物理電與磁的一些要點，只會記錄常用公式和右手指向的一些規律
  • 以下都是參考網上教材

磁力線特性

  1. 由法拉第提出的一假想曲線
  2. 在磁鐵外部由 N 極射出指向 S 極,再經磁鐵內部由 S 極回到 N 極,形成一封閉曲線。
  3. 磁力線的切線方向,代表該點之磁場方向,亦即磁針 N 極所指的方向;互相排斥,永不相交。
  4. 磁場的量值與磁力線密度成正比。

電流的磁效應

  1. 1820 年丹麥物理學家 厄斯特首先發現載流導線附近的磁針會受影響而偏轉,表示載流導線的周圍會產生磁場,此現象稱為電流的磁效應。
  2. 一週後法國物理學家 安培 提出電流與所產生磁場方向的關係「安培右手定則」: 以右手握住長直導線,拇指指向電流方向,則其他四指彎曲為磁場在導線四周的方向。

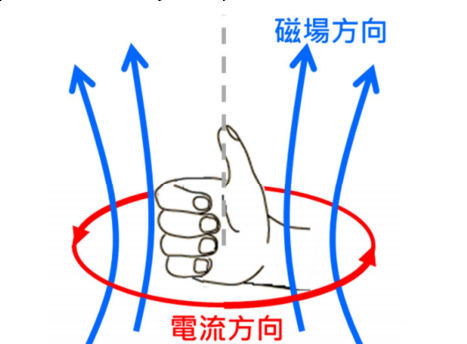
圖 1

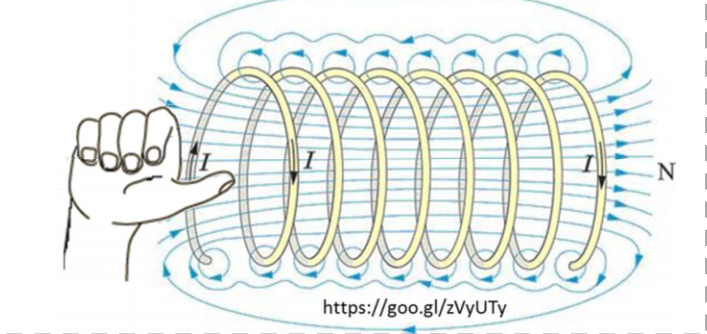
圖 2

必歐-沙伐定律

  1. 微分積分概念下的必歐-沙伐定律, 請參考wiki
  2. 必歐-沙伐兩人由實驗驗証了載流長直導線四周的磁場與通過的電流大小成正比,與導線的垂直距離$r$成反比 $B \propto \frac{1}{r}$, 並由此推出必歐-沙伐定律。

特別程況的電流單位元所貢獻的磁場$\Delta \vec{B}$，如下圖:


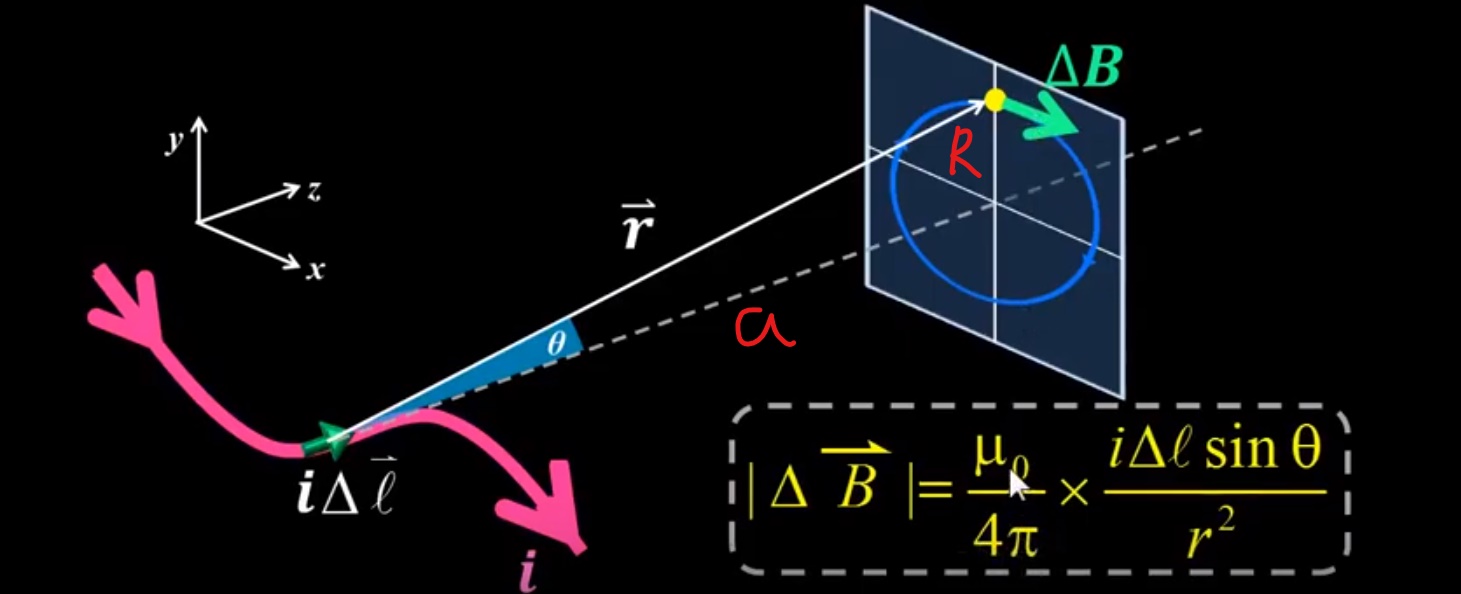
圖 3
\[\begin{align} \label{Biot-Savart Law vector} \Delta\vec{ B} &=\frac{\mu_0}{4 \pi} \frac{i \Delta\vec{ l} \times \vec{r} } {r^3} \\ \label{Biot-Savart Law} \vert \Delta\vec{ B} \vert &=\frac{\mu_0}{4 \pi} \frac{i \Delta\vec{ l} \sin \theta}{r^2} \ \end{align}\]

其中， \(\begin{aligned} B &: \text{電流元於P點共獻的磁場}(T) \\ i &: \text{導體上的電流}(A) \\ \Delta l &: \text{電流元的長度}(m) \\ r &:\text{某點P到電流元的長度}(m) \\ \mu_0 &:\text{磁常數} = 4\pi \times 10^{-7} (N/A^2 \quad \text{or} \quad T \dot m/A) \end{aligned}\)

當中$P$點共獻的磁場的方向是

  1. $\Delta \vec{l} \times \vec{r}$
  2. 右手安培定則

載流長直導線建立的磁場

Ref:link


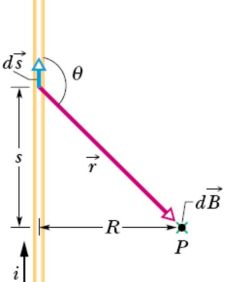
圖 7
\[\begin{aligned} B &=\int dB=\int \frac{\mu_0}{4 \pi} \frac{i ds \sin \theta}{r^2} \\ &=\int\limits_{-\infty}^{\infty} \frac{\mu_0}{4 \pi} \frac{i ds R}{(R^2+s^2)^{3/2}} ds \\ &=\frac{\mu_0 i}{2\pi R}\left(\frac{s}{(s^2+R^2)^{1/2}} \right)\Bigg\vert_0^{\infty} \\ &=\frac{\mu_0 i}{2\pi R} \end{aligned}\]

載流圓線圈中心軸一點P的磁場

如圖 3

\[\begin{aligned} \int \Delta \vec{B} &=\sum \frac{\mu_0}{4 \pi} \frac{i \Delta\vec{ l} \sin \theta}{r^2} \\ &=\frac{\mu_0}{4 \pi} \frac{i \sum (\Delta\vec{ l}) \sin \theta}{r^2} \\ &=\frac{\mu_0}{4 \pi} \frac{i (2\pi R)(\frac{R}{r})}{r^2}\\ &=\frac{\mu_0 i R^2}{2r^{3}} \\ &=\frac{\mu_0 i R^2}{2(R^2+a^2)^{3/2}} \end{aligned}\]

載流螺絲管內建立的磁場

  1. 磁場線: 如圖 2
  2. 磁場大小:
\[B=\mu_0 N i\]

其中$N$是單位長度(m)內的匝數

載流導線在磁場中所受的磁力


圖 5
  1. 大小：

\begin{equation} \label{ilB} F=i\vec{l}\times \vec{B}=i l_{\bot} B=ilB\sin \theta,\end{equation}

其中$\theta$是導線與磁場的夾角。

  1. 方向:

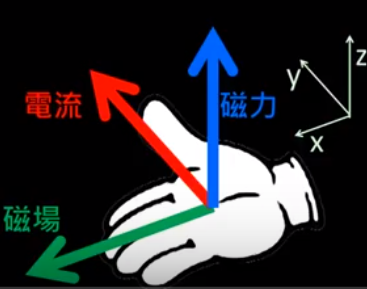
圖 4

兩平行載流長直導間的磁力


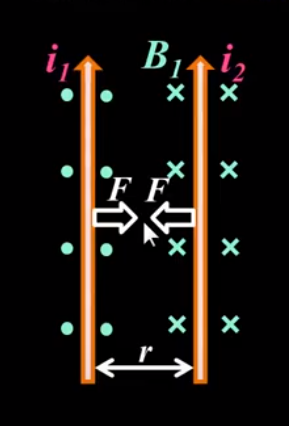
圖 6
\[\begin{aligned} F_2 &=i_2 \times l \times B_1=i_2 \times l \times \frac{\mu_0 i_1}{2\pi r} \\ F_1 &=i_1 \times l \times B_2=i_1 \times l \times \frac{\mu_0 i_2}{2\pi r} \\ \implies F_1&=F_2=\frac{\mu_0 i_1 i_2 l}{2 \pi r} \end{aligned}\]

電動機

  • 力矩；wiki
  • $\vec{\tau}=r \times F$

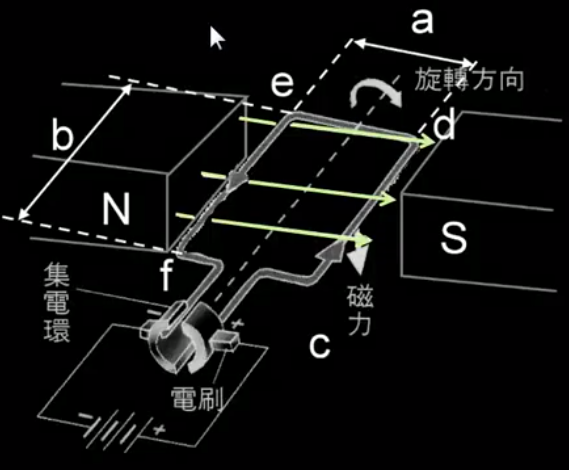
圖 8

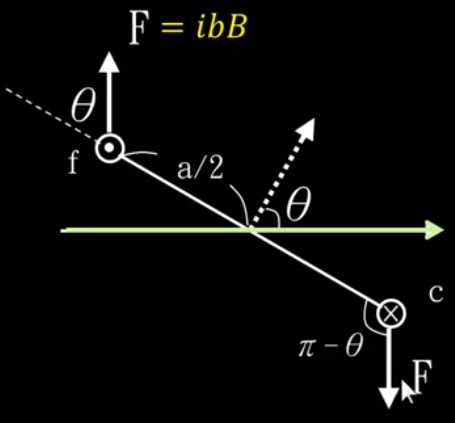
圖 9
  1. 閉合方形迴路在磁場受到的合力為零:$\sum \vec{F}=0$
  2. 總力矩：
\[\begin{aligned} \sum\vec{\tau}&= F \times \frac{a}{2} \sin \theta \times 2\\ &= ibB \times a \sin \theta \\ &=iBA \sin \theta \\ \end{aligned}\]

其中，$A$是線圈的面積, $\theta$ 是力與向心方向的夾角。

帶電質點在磁場中的運動

勞侖茲力:

  1. 1892 年,荷蘭物理學家 勞侖茲 提出,帶電粒子在磁場中運動時會受到一力作用, 其力的大小與磁場,粒子的帶電量、及垂直於磁場的速度成正比。

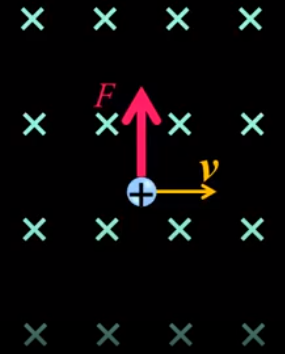
圖 10
  1. 性質:由數學上外積的特性可看出勞倫茲力的方向總與運動方向垂直, 所以勞倫茲力永不做功,只改變帶電粒子的運動方向。

\begin{equation} \label{Lorentz force} F=q\vec{v}\times \vec{B}=qvB\sin\theta=qv_{\bot}B=qvB_{\bot} \end{equation}

由 $\eqref{ilB}$ 推導出 $\eqref{Lorentz force}$

\[\begin{aligned} \vec{F}&=i\vec{l}\vec{B}\\ &=\frac{q}{\Delta t}( v\Delta t )\times \vec{B} \\ &= q\vec{v}\times \vec{B} \end{aligned}\]

$\vec{v}\bot \vec{B}$

因為勞侖茲力 只改變帶電粒子的運動方向，所以 當$\vec{v}\bot \vec{B}$時， 勞侖茲力等於向心力。

向心力

  • wiki
  • $F=m\omega^2 r=m\frac{v^2}{r^2}r=m\frac{v^2}{r}$
\[\begin{aligned} F&=qvB=m\frac{v^2}{R} \end{aligned}\]

\begin{equation} \label{Radius} \implies R=\frac{mv}{qB} =\frac{\sqrt{2mE_k}}{qB}=\frac{\sqrt{2mqV}}{qB} \end{equation}

\begin{equation} \label{Period} \implies T=\frac{2\pi R}{v}=\frac{2\pi m}{qB} \end{equation}

由電位能$qV$轉成動能$E_k$，所以能調整電壓$V$來控制粒子速度$v$。

$\vec{v}$與$ \vec{B} $夾角為$\theta\neq 0,90,180,270$


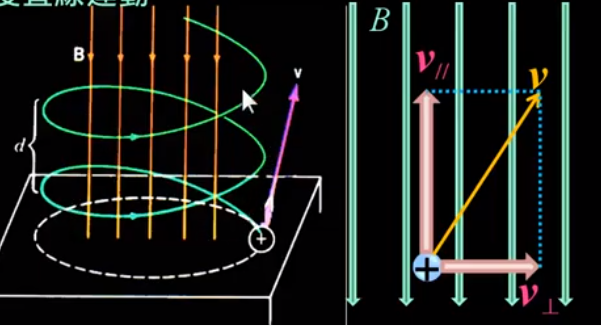
圖 10

$v$分解為兩個分量$v_0$和$v_{\bot}$

  1. $v_0$：等速直線運動
  2. $v_{\bot}$：等速圖週運動

由以上分析：粒子是以螺線形軌跡運動
螺距$d$:螺釘旋轉一周前進之距離

\[d=v_0 \times T=v\cos \theta \times \frac{2 \pi m}{ qB} \quad \text{by } \eqref{Period}\]

速度選擇器

  • 可篩選出具有某特定速度之帶電粒子之儀器
  • 結構:內部具有相互垂直的電磁場

圖 12

只有速度

\begin{equation} \label{select v} v_0=\frac{E_0}{B_0} \end{equation}

才會出來。

質譜儀


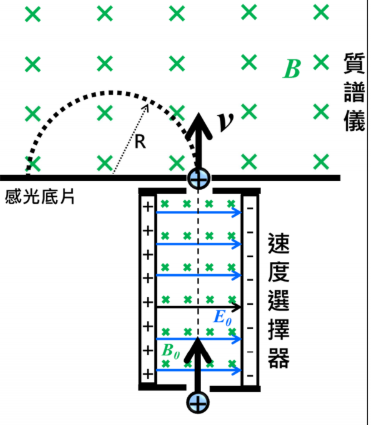
圖 13

by $\eqref{Radius}$ 和 $\eqref{select v}$

\[R=\frac{mv}{qB}=\frac{mE_0}{qBB_0}\]

You May Also Enjoy