• 庫侖力
• 電場
  • 電力線
  • 帶靜電導體的電力線及電場特性
  • 帶靜電「對稱導體球」所建立的電場
  • 均勻帶電平行板的電場
• 電位能與電位
  • 電位能
  • 電位：

庫侖力

\begin{equation} \label{Coulomb’s law} F_e=\frac{kQq}{r^2} \end{equation}

其中，$k=8.99\times 10^9 N\cdot m^2/C^2$

電場

-單位電荷於該處所受之電力(為一向量)

在$q$電荷所產生電場

\begin{equation} \label{elec field} E=\frac{F_e}{q}=\frac{kQ}{r^2} \end{equation}

電力線

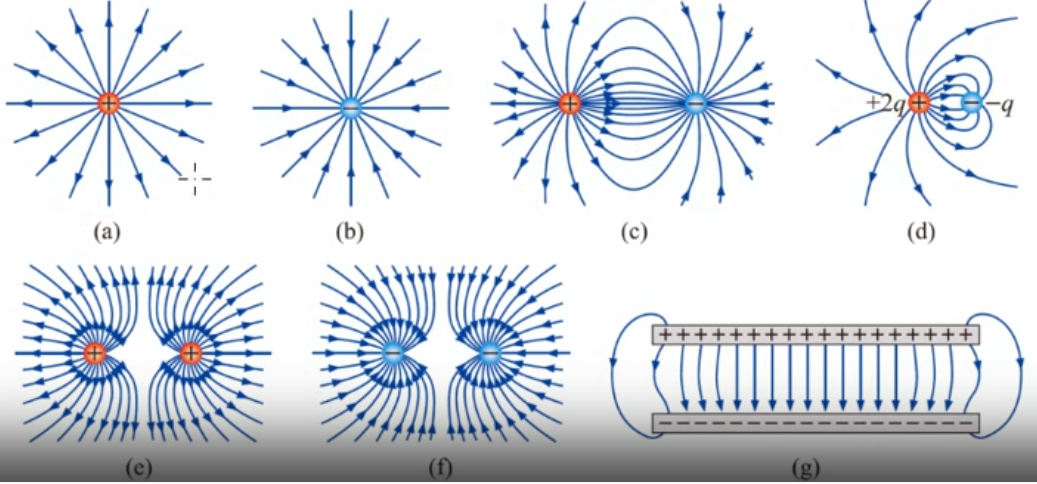
圖 1:電力線

1. 正電荷的電力線朝外,負電荷的電力線朝內
2. 始於正電荷,終於負電荷,為一開放曲線,且永不相交
3. 空間中某處的電力線密度,代表該處電場大小
4. 電力線上任一點的切線方向等於該點「正」電荷所受電力方向(即電場方向)

帶靜電導體的電力線及電場特性

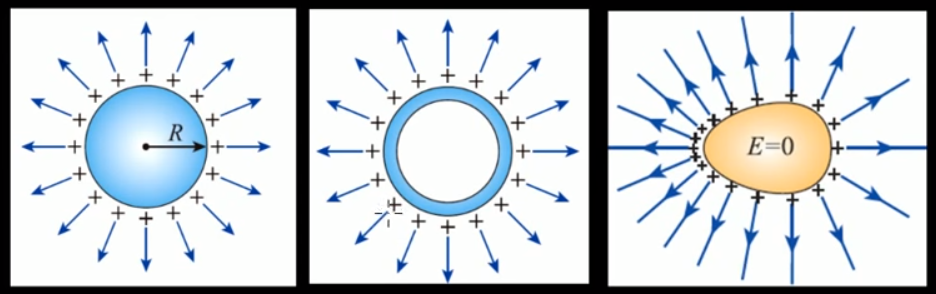
圖 2:帶靜電導體

若內部有電場，內部電荷就會受力移動，便與靜電這一特性矛盾，所以

1. 帶靜電導體內部必無淨電荷,故內部電場為零 若電力線不垂直表面，會有平行方向的分量，就會在表面移動，便與靜電這一特性矛盾，所以
2. 電荷分佈於外表面,且電力線垂直於導體表面

帶靜電「對稱導體球」所建立的電場

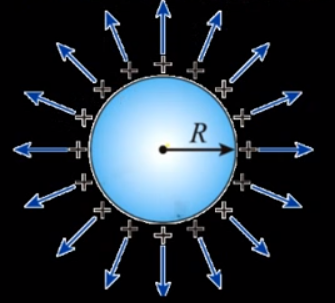
圖 3:帶靜電對稱導體球

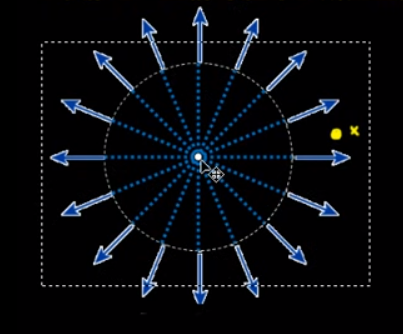
圖 4:點電荷電場

1. 由外側觀察其電力線分佈情形,與所發出的電力線相同。
2. 故可將其電荷視為集中在球心

均勻帶電平行板的電場

1. 無窮大之均勻帶電平板周遭的電場:
   • 板附近任意點之電場 E 為定值,與距離無關
2. 均勻帶電平行板間的電場:
   • 板內提供均勻電場

電位能與電位

電位能

• 電位能:兩點電荷間所儲存之能量(為純量)外力抵抗「電力」所作的功儲存而成

其中，$W_e$是電力所做的功，$W_F$是外力所做的功

電位：

• 為形容電位能而提出之輔助物理量
• 類似重力位能之高度，為一相對值
• 物理意義：某處電位＝單位正電荷在該點所具有的電位能(為一純量)
• 在電荷$q$點的電位是:

\begin{equation} \label{V U relation} \bar V=\frac{U_e}{q} \quad (\text{V or } \frac{j}{C}) \end{equation}