• Naive Bayes Algorithm
  • Bayes’ Rule
  • The Bayes’ Classifier
  • Naive Bayes Algorithm
  • Likelihood Function
  • Example
  • python code

Naive Bayes Algorithm

• Basically, this is my studying from NTCU open course - Machine Learning. I take the key points for my references.

Bayes’ Rule

Assume that ${B_i, i=1,\dots,n}$ is a partition of $S$ such that $P(B_i)>0 \text{ for } i=1,2,…,k$. Then

The Bayes’ Classifier

• For choose $i$ such that $P(C_i \vert x)$ is maximum is irrelevant with the value of $P(x)$.

Naive Bayes Algorithm

• Two not reasonalbe assumptions
  • The importance of each of attribute is equal
  • All attributes are conditional probability independent.

Likelihood Function

• ex. a baised coin flip $N$ times, and we could use MLE(Maximum Likelihood Estimates) to estimate the probability $p$ of coin with positive side.

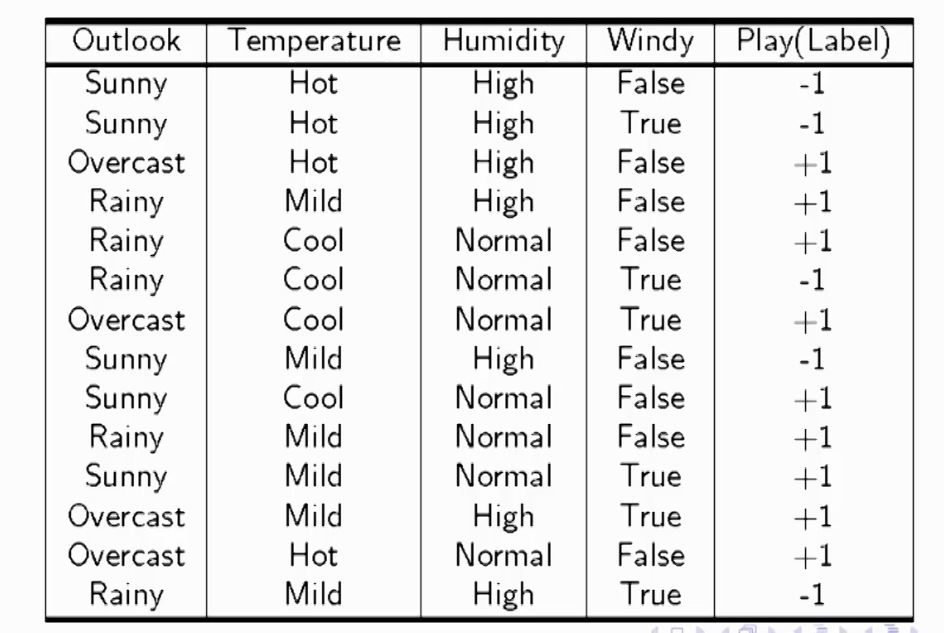
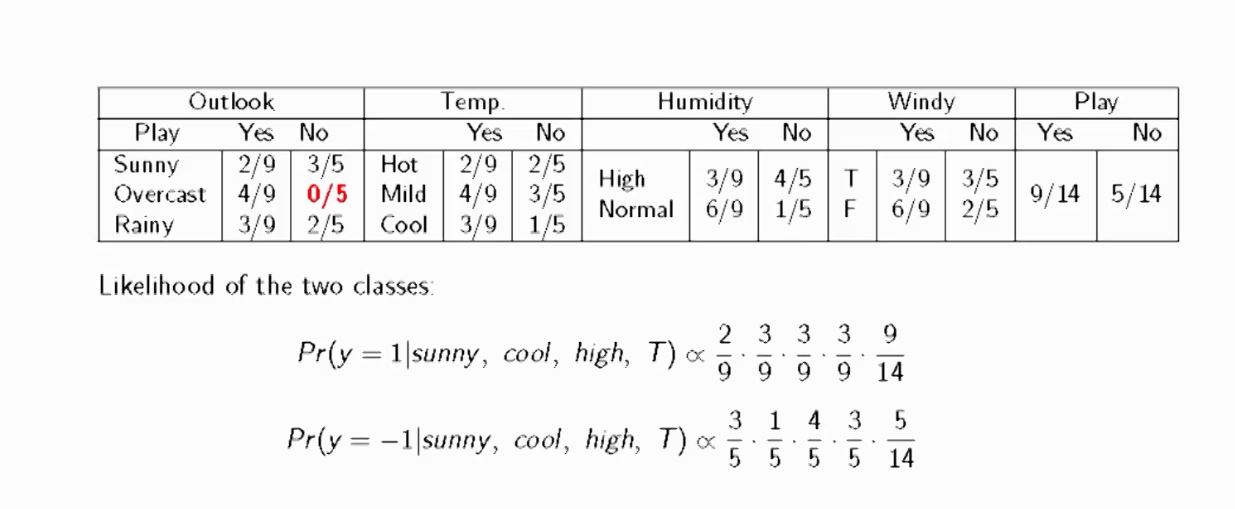
Example

• The above images are captured from link

python code

• This is from website

  weather=['Sunny','Sunny','Overcast','Rainy','Rainy','Rainy','Overcast','Sunny','Sunny',
  'Rainy','Sunny','Overcast','Overcast','Rainy']
  temp=['Hot','Hot','Hot','Mild','Cool','Cool','Cool','Mild','Cool','Mild','Mild','Mild','Hot','Mild']
  play=['No','No','Yes','Yes','Yes','No','Yes','No','Yes','Yes','Yes','Yes','Yes','No']
  

• Encoding Features

  # Import LabelEncoder
  from sklearn import preprocessing
  #creating labelEncoder
  le = preprocessing.LabelEncoder()
  # Converting string labels into numbers.
  weather_encoded=le.fit_transform(weather)
  print weather_encoded
  

  temp_encoded=le.fit_transform(temp)
  label=le.fit_transform(play)
  print "Temp:",temp_encoded
  print "Play:",label
  features=zip(weather_encoded,temp_encoded)
  print features
  

• Perform prediction

  #Import Gaussian Naive Bayes model
  from sklearn.naive_bayes import GaussianNB
  #Create a Gaussian Classifier
  model = GaussianNB()
  # Train the model using the training sets
  model.fit(features,label)
  #Predict Output
  predicted= model.predict([[0,2]]) # 0:Overcast, 2:Mild
  print "Predicted Value:", predicted