Lat Lon distance

Let \(\text{lat} =\phi\) \(\text{lon}=\lambda\) \(R = \text{the radiance of earth}\) 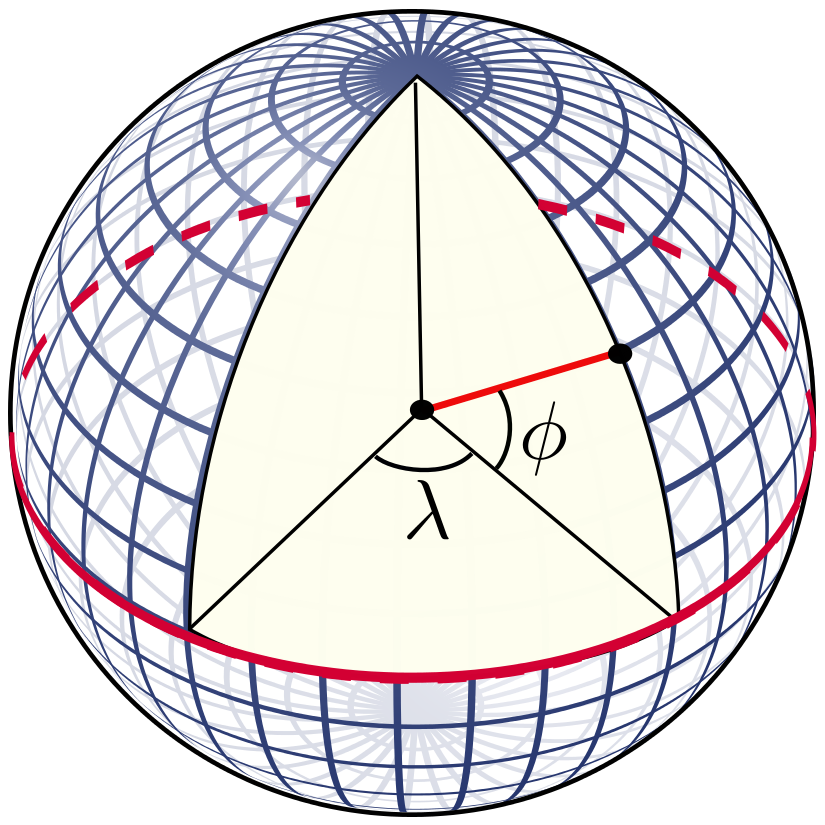Therefore, the length of equator be $ 2\pi R$, and the distance of 1 deg at equator is $ \frac{\pi}{180}R$.

Moreover, the the distance of the circle of latitude at $ \text{lat} =\phi$ is \(\displaystyle \cos(\phi) 2\pi R.\)

This can be interpreted as the circle of latitude at $ \text{lat} =\phi$ project to equatorial plane and this is the reason why we multiply the scalar $ \displaystyle \cos(\phi)$.

Consequencely, the length of 1 degree lon at $ \displaystyle \cos(\phi)$ is \(\cos(\phi)\times \frac{\pi}{180}R \approx \cos(\phi)*111 (km).\)